Abi 2015 Analysis II Teil B: Unterschied zwischen den Versionen
K |
|||
| Zeile 24: | Zeile 24: | ||
Gegeben ist die Funktion f mit <math> f(x)=\frac{1}{x+1} - \frac{1}{x+3}</math> und Dafinitionsbereich D<sub>f</sub> = IR \ {-3;-1}. Der Graph von f wird mit G<sub>f</sub> bezeichnet. | Gegeben ist die Funktion f mit <math> f(x)=\frac{1}{x+1} - \frac{1}{x+3}</math> und Dafinitionsbereich D<sub>f</sub> = IR \ {-3;-1}. Der Graph von f wird mit G<sub>f</sub> bezeichnet. | ||
| − | a) | + | a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist: |
| − | + | ||
| − | Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist: | + | |
<math> \frac{2}{(x+1)(x+3)} ; \frac{2}{x^2+4x+3} ; \frac{1}{0,5*(x+2)^2-0,5}</math> | <math> \frac{2}{(x+1)(x+3)} ; \frac{2}{x^2+4x+3} ; \frac{1}{0,5*(x+2)^2-0,5}</math> | ||
| − | b) | + | b) Begründen Sie, dass die x-Achse horizontale Asymptote von G<sub>f</sub> ist, und geben Sie die Gleichung der vertikalen Asymptoten von G<sub>f</sub> an. Bestimmen Sie die Koordinaten des Schnittpunktes von G<sub>f</sub> mit der y-Achse. |
| − | + | ||
| − | Begründen Sie, dass die x-Achse horizontale | + | |
| − | Asymptote von G<sub>f</sub> ist, und geben Sie die Gleichung der vertikalen Asymptoten von G<sub>f</sub> an. Bestimmen Sie die Koordinaten des Schnittpunktes von G<sub>f</sub> mit der y-Achse. | + | |
Abbildung 1 zeigt den Graph der in IR definerten Funktion p:x > 0,5*(x+2)<sup>2</sup> -0,5, die die Nullstelle x=-3 und x=-1 hat. | Abbildung 1 zeigt den Graph der in IR definerten Funktion p:x > 0,5*(x+2)<sup>2</sup> -0,5, die die Nullstelle x=-3 und x=-1 hat. | ||
| − | Für | + | Für x ∈ D<sub>f</sub> gilt <math>f(x)=\frac{1}{p(x)}</math>. |
'''GRAPHIK EINFÜGEN''' | '''GRAPHIK EINFÜGEN''' | ||
| − | c) | + | c) Gemäß der Quotientenregel gilt für die Ableitung f' und p' die Beziehung <math> f'(x)=-\frac{p'(x)}{(p(x))^2}</math> für x ∈ D<sub>f</sub> |
| − | + | ||
| − | Gemäß der Quotientenregel gilt für die Ableitung f' und p' die Beziehung <math> f'(x)=-\frac{p'(x)}{(p(x))^2}</math> für | + | |
Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x=-2 einzige Nullstelle von f' ist und dass G<sub>f</sub> in ]-3;-2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunktes von G<sub>f</sub> an. | Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x=-2 einzige Nullstelle von f' ist und dass G<sub>f</sub> in ]-3;-2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunktes von G<sub>f</sub> an. | ||
| − | d) | + | d) Berechnen Sie f(-5) und f(-1,5) und skizzieren Sie G<sub>f</sub> unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1. |
| − | + | ||
| − | Berechnen Sie f(-5) und f(-1,5) und skizzieren Sie G<sub>f</sub> unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1. | + | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 73: | Zeile 64: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | |||
Gegeben ist die Funktion <math> h(x)= \frac{3}{e^{x+1} -1}</math> mit Definitionsbereich D<sub>h</sub> = ]-1;+∞[. Abbildung 2 zeigt den Graph G<sub>h</sub> von h. | Gegeben ist die Funktion <math> h(x)= \frac{3}{e^{x+1} -1}</math> mit Definitionsbereich D<sub>h</sub> = ]-1;+∞[. Abbildung 2 zeigt den Graph G<sub>h</sub> von h. | ||
Version vom 23. Juli 2017, 21:22 Uhr
|
|
Gegeben ist die Funktion f mit a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
Abbildung 1 zeigt den Graph der in IR definerten Funktion p:x > 0,5*(x+2)2 -0,5, die die Nullstelle x=-3 und x=-1 hat. Für x ∈ Df gilt GRAPHIK EINFÜGEN
Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x=-2 einzige Nullstelle von f' ist und dass Gf in ]-3;-2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunktes von Gf an.
|
Gegeben ist die Funktion
|
Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen Definitionsmenge die angegebenen Eigenschaften besitzt. a) Der Graph der Funktion f ist achsensymmetrisch zur y-Achse und die Gerade mit der Gleichung x = 2 ist eine senkrechte Asymptote. b) Die Funktion g ist nicht konstant und es gilt g x dx 0. |
An einer Messstation wurde über einen Zeitraum von 10 Stunden die Anzahl der Pollen in einem Kubikmeter Luft ermittelt. Dabei kann die Anzahl der Pollen in einem Kubikmeter Luft zum Zeitpunkt t (in Stunden nach Beginn der Messung) durch die Gleichung 2 n t 3t 60t 500 beschrieben werden. a) Bestimmen Sie die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung. b) Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft 1 h 30 beträgt. |
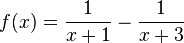 und Dafinitionsbereich Df = IR \ {-3;-1}. Der Graph von f wird mit Gf bezeichnet.
und Dafinitionsbereich Df = IR \ {-3;-1}. Der Graph von f wird mit Gf bezeichnet.
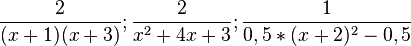
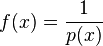 .
.
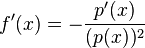 für x ∈ Df
für x ∈ Df

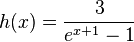 mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.




