Stochastik

Zu Aufgabe 1

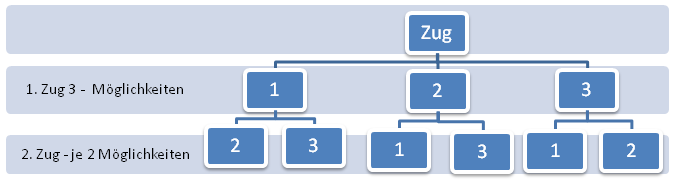
• Ganz einfach, man erstellt sich ein Baumdiagramm nennt die Kugeln bspweise 1,2 und 3,

• also ist der Ergebnissraum Ω = { 123,132,213,231,312,321 }

• (bekomme keine geschweiften Klammern hin) und damit ist die Mächtigkeit |Ω|= $2*3 = 6$

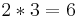
• Hier nochmal das Baumdiagramm:

Zu Aufgabe 2

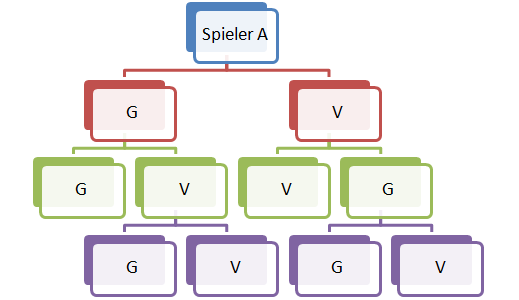
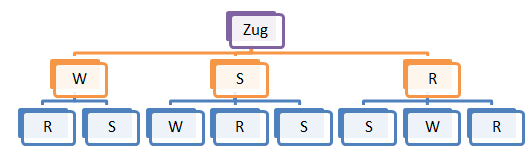
• Eigentlich auch ganz einfach, man hat 2 Tennisspieler, die 2 Sätze spielen, Sieger ist derjenige, der als erster 2 Sätze gewonnen hat!

• Also ist der Ergebnissraum wenn man Spieler 1 als A und Spieler 2 als B nennt und einen Satzsieg als G, eine Satzniederlage als V bezeichnet.

Ω = {AGG,AGVG,AGVV,AVV,AVGV,AVGG}

• Und damit ist die Mächtigkeit |Ω|= 2*1+4 = 6 danke an Burkard xD

Zu Aufgabe 4

• Weiße Kugel= W, Schwarze Kugel=S!

a)

• Eine Urne mit 3 weißen und 2 schwarzen Kugeln, es werden gleichzeitig 3 Kugeln der Urne entnommen. Ein Ergebnissraum wäre z.B

Ω = {WWW,WWS,WSS}

also wäre die Mächtigkeit |Ω|= 3*1 = 3

b)

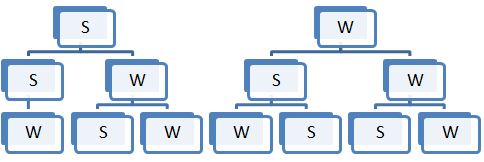
• Nun werden die 3 Kugeln nacheinander ohne zurücklegen herausgenommen!

Ein Ergebnissraum wäre z.BΩ = {WWW,WWS,WSS,WSW,SWS,SSW,SWW} folglich ist die Mächtigkeit dann |Ω|= 2*2+3

c)

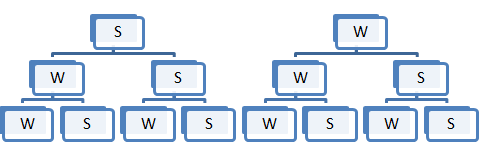
• Teilaufgabe c) ist eigentlich die selbe Aufgabenstellung wie b) nur dass diesmal jede Kugel, die gezogen wurde wieder zurückgelegt wird.

Ein Ergebnissraum wäre z.BΩ = {WWW,WWS,WSW,WSS,SSS,SSW,SWW,SWS}

folglich ist die Mächtigkeit dann |Ω|= 2*2*2=8

Zu Aufgabe 5

• Ein Würfel wird solange geworfen bis 6 erscheint aber höchstens 3 mal, sonst würden die Möglichkeiten ins Unendliche gehn, da ja theoretisch die 6 nie auftauchen könnte ! Ausgenommen ist der Fall, dass der Würfel auf der Kante liegen bleibt!

• Dann ist ein möglicher Ergebnissraum Ω = {1,2,3,4,5,6,1-1,1-2,1-3...1-6,1-1-1,1-1-2,1-1-3...1-1-6}

Mächtigkeit ist etwas knifflig |Ω|= 5*5*5+(1+5+25)=156

Zu Aufgabe 6

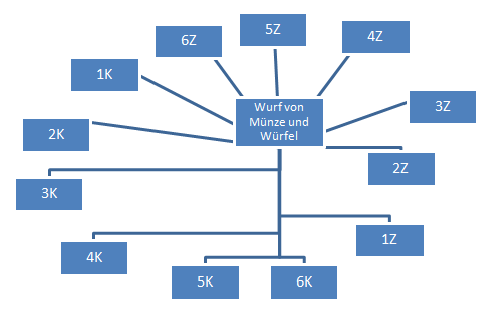
• Situation: Eine Münze und ein Würfel werden geworfen und man soll den Ergebnissraum darstellen - dieser ist:

• Ω = {1K,2K,3K,4K,5K,6K,1Z,2Z,3Z,4Z,5Z,6Z}

• Mächtigkeit ist somit |Ω|= 6*2=12

• Man geht davon aus, dass der Würfel oder die Münze auf einer geraden Oberfläche geworfen werden und dass beide nicht auf der Kante liegen bleiben! K steht für Kopf, Z steht für Zahl!

Zu Aufgabe 7

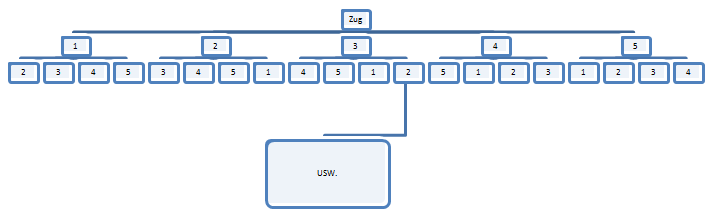
• In einer Urne befinden sich fünf von 1 bis 5 nummerierte Urnen! Es werden 2 Kugeln gezogen

a) nacheinander ohne zurücklegen

• Eigentich einfach ein möglicher Ergebnissraum wäre dann

• Möglicher Ergebnissraum wäre dann Ω = {12,13,14,15,21,22,23...51,52,53,54}

• Bei der ersten Kugel gib es 5 Möglichkeiten welche Kugel man erwischt nämlich Kugel 1,2,3,4 oder 5 dann gibt es nochmal jeweils 4 Möglichkeiten bei Kugel 1 z.B die Möglichkeit als nächstes Kugel 2,3,4 oder 5 zu ziehen.

• Mächtigkeit ist |Ω|= 5*4=20

b) Gleichzeitiges Ziehen von 3 Kugeln

Splitten wir es mal auf und tuen so, als ob jede Kugel einzeln gezogen wird jedoch nicht mehr zurücggelegt wird. Dann gibt es am Anfang mit dem Zug der ersten Kugel 5 Möglichkeiten, beim 2ten Zug noch jeweils 4 und beim 3ten Zug noch jeweils 3!

• Möglicher Ergebnissraum wäre dann Ω = {123,124,125...543}

• Mächtigkeit ist |Ω|= 5*4*3=60 ist die 3fache Mächtigkeit dessen, was bei a) als Mächtigkeit stand

Zu Aufgabe 8

1 Weiße, 2 Schwarze und 3 Rote Kugeln es werden 2 Kugeln gezogen und zwar:

a) nacheinander ohne zurücklegen

• Ein möglicher Ergebnissraum wäre dann: Ω = {WR,WS,SS,SW,SR,RR,RS,RW}

• Somit ist die Mächtigkeit |Ω|= 2*3+1*2=8

b) nacheinander mit zurücklegen

Eigentlich dasselbe wie bei a) nur, dass es auch die Möglichkeit gibt die einzelne weiße Kugel 2 mal zu ziehen.

• Ein möglicher Ergebnissraum wäre dann: Ω = {WW,WR,WS,SS,SW,SR,RR,RS,RW}

• Mächtigkeit in diesem Fall |Ω|= 3*3=9

Aufgabe 3 und Aufgabe 7 wird noch am Wochenende hochgeladen - hoffentlich!