Abi 2017 Analysis II Teil A
Aus RMG-Wiki
< Abitur Mathematik
Version vom 28. März 2018, 12:27 Uhr von Karina Hetterich (Diskussion | Beiträge)
|
|
Gegeben ist die Funktion f mit a) Geben Sie D und die Koordinaten der Schnittpunkte von Gf mit den Koordinatenachsen an. b) Zeigen Sie, dass f(x) zum Term
|
Eine Funktion f ist durch a) Ermitteln Sie die Nullstelle der Funktion f. b) Die Tangente an den Graphen von f im Punkt S(0 |1) begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. |
Die Abbildung zeigt den Graphen der in IR definierten Funktion |
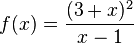 und maximalem Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.
und maximalem Definitionsbereich D. Der Graph von f wird mit Gf bezeichnet.
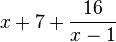 äquivalent ist, und geben
Sie die Bedeutung der Geraden g mit der Gleichung y=x+7 für Gf an.
äquivalent ist, und geben
Sie die Bedeutung der Geraden g mit der Gleichung y=x+7 für Gf an.
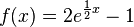 mit x ∈ IR gegeben.
mit x ∈ IR gegeben.
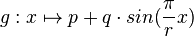 mit p,q,r,∈IN.
mit p,q,r,∈IN.

