Abi 2015 Analysis I Teil B
|
|
Gegeben ist die Funktion f mit
b) Begründen Sie, dass die x-Achse horizontale Asymptote von Gf ist, und geben Sie die Gleichungen der vertikalen Asymptoten von Gf an. Be-
stimmen Sie die Koordinaten des Schnittpunkts von Gf mit der y-Achse. Abbildung 1 zeigt den Graphen der in IR definierten Funktion Für x ∈ Df gilt c) Gemäß der Quotientenregel gilt für die Ableitungen f' und p' die Beziehung: Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x = -2 einzige Nullstelle von f' ist und dass Gf in ]-3; -2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von Gf an. d) Berechnen Sie f(-5) und f(-1,5) und skizzieren sie Gf unter Berücksichtigung der Ergebnisse in Abbildung 1. |
Gegeben ist die Funktion a)
Begründen Sie anhand des Funktionsterms, dass b) Begründen Sie ohne weitere Rechnung, dass folgende Aussagen wahr sind:
c) Geben Sie die Nullstelle von H0 an und bestimmen Sie näherungsweise mithilfe von Abbildung 2 die Funktionswerte H0 (-0,5) sowie H0 (3). Skizzieren Sie in Abbildung 2 den Graphen von H0 im Bereich -0,5 ≤ x ≤ 3.
|
In einem Labor wird ein Verfahren zur Reinigung von mit Schadstoffen kontaminiertem Wasser getestet. Die Funktion h aus Aufgabe 2 beschreibt für x ≥ 0 modellhaft die zeitliche Entwicklung des momentanen Schadstoffabbaus in einer bestimmten Wassermenge. Dabei bezeichnet h(x) die momentane Schadstoffabbaurate in Gramm pro Minute und x die seit Beginn des Reinigungsvorgangs ergangene Zeit in Minuten. a) b) Beschreiben Sie, wie der Graph der Funktion k aus dem Graphen der Funktion f aus Aufgabe 1 hervorgeht. c)
|
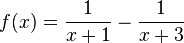 und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
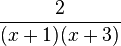 ;
;
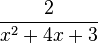 ;
;
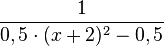

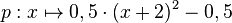 , die die Nullstellen x = -3 und x = -1 hat.
, die die Nullstellen x = -3 und x = -1 hat.
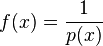 .
.

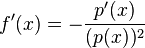 für x ∈ Df.
für x ∈ Df.


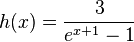 mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
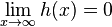 gilt. Zeigen Sie rechnerisch für x ∈ Dh, dass für die Ableitung h′ von h gilt: h′(x)<0.
Gegeben ist ferner die in Dh definierte Integralfunktion H0:
gilt. Zeigen Sie rechnerisch für x ∈ Dh, dass für die Ableitung h′ von h gilt: h′(x)<0.
Gegeben ist ferner die in Dh definierte Integralfunktion H0: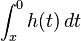 .
.

