Abi 2012 Analysis I Teil B
|
|
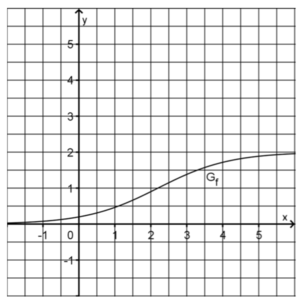
Gegeben ist die Funktion a) Zeigen Sie rechnerisch, dass Gf genau einen Achsenschnittpunkt S besitzt und geben Sie die Koordinaten von S an. b) Begründen Sie mithilfe des Funktionsteams von f, dass c) Weisen Sie rechnerisch nach, dass Gf in IR streng monoton steigt. d) Bestimmen Sie die Gleichung der Tangente an Gfim Achsenschnittpunkt S. e) Berechnen Sie den Inhalt der Fläche, die Gf mit den Koordinatenachsen und der Geraden x=4 einschließt. f) Begründen Sie, dass f in IR umkehrbar ist. Gebe Sie den Definitionsbereich und den Wertebereich der Umkehrfunktion f-1 an und zeichnen Sie den Graphen von f-1 in Abbildung 2 ein.
|
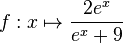 mit Definitionsbereich IR. Abbildung 2 zeigt den Graphen Gf von f.
mit Definitionsbereich IR. Abbildung 2 zeigt den Graphen Gf von f.

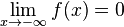 und
und 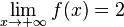 gilt.
gilt.

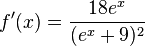 )
)


