Abi 2012 Analysis I Teil A

Mathematik (Bayern): Abiturprüfung 2012 Analysis I - Teil A Download der Originalaufgaben - Lösung zum Ausdrucken

Aufgabe 1 Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion an. a) $f(x) = ln(x+3)$ b) $g(x) = \frac{2}{x^{2}-1}$ [Lösung anzeigen][Lösung ausblenden] 700px

Aufgabe 2 Geben Sie jeweils den Term einer in IR definierten Funktion an, die die angegebene Eigenschaft besitzt. a) Der Graph der Funktion f hat den Hochpunkt (0|5) . b) Die Funktion g ist an der Stelle x = 5 nicht differenzierbar. [Lösung anzeigen][Lösung ausblenden] 700px

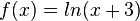
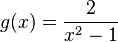
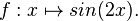
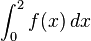Aufgabe 3 Gegeben ist die in IR definierte Funktion $f:x \mapsto sin(2x).$ a) Geben Sie zwei benachbarte Nullstellen von f an. b) Berechnen Sie den Wert des bestimmten Integrals $\int_{0}^{2} f (x)\,dx$. Warum stimmt der Wert diese Integrals ich mit dem Inhalt der Fläche überein, die für 0 ≤ x ≤ 2 zwischen dem Graphen von f und der x-Achse liegt? [Lösung anzeigen][Lösung ausblenden] 700px

Aufgabe 4 [Lösung anzeigen][Lösung ausblenden] 700px