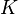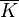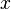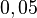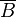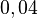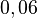Abituraufgaben zu bedingten Wahrscheinlichkeiten
alle Aufgaben als pdf-Datei
Originalaufgaben zum Download oder Ausdrucken
Aufgabe 1: Abitur 2014 - 1A
Quelle: ISB
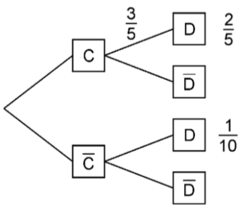
Das Baumdiagramm gehört zu einem Zufallsexperiment mit den Ereignissen C und D.
1a) Berechnen Sie 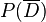 .
.
ausführliche Lösung
Aufgabe 2: Abitur 2014 - 1B
Quelle: Originalaufgabe
Im Rahmen der sogenannten JIM-Studie wurde in Deutschland im Jahr 2012 der Umgang von Jugendlichen im Alter von 12 bis 19 Jahren mit Information und Medien untersucht. In der folgenden Tabelle werden ausgewählte Ergebnisse dieser Studie anhand einer repräsentativen Auswahl von 200 Jugendlichen wiedergegeben, von denen 102 Jungen sind. Dabei werden für vier Geräteklassen jeweils die Anzahl der Mädchen und die Anzahl der Jungen unter den 200 ausgewählten Jugendlichen angegeben, die ein entsprechendes Gerät besitzen.
(Tabelle ergänzen)
1 a) Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine aus den 200 Jugendlichen zufällig ausgewählte Person weiblich ist und kein Fernsehgerät besitzt.
1 b) Aus den 200 Jugendlichen wird eine Person zufällig ausgewählt, die ein Fernsehgerät besitzt. Ermitteln Sie die Wahrscheinlichkeit dafür, dass diese Person weiblich ist.
ausführliche Lösung
Aufgabe 3: Abitur 2013 - 1
Quelle: ISB
Bei 0,074 % der neugeborenen Kinder liegt eine bestimmte Stoffwechselstörung vor. Wird diese Störung frühzeitig erkannt, lässt sich durch eine geeignete Behandlung eine spätere Erkrankung vermeiden. Zur Früherkennung kann zunächst ein einfacher Test durchgeführt werden. Zeigt das Ergebnis des Tests die Stoffwechselstörung an, so bezeichnet man es als positiv. Liegt bei einem neugeborenen Kind die Stoffwechselstörung vor, so ist das Testergebnis mit einer Wahrscheinlichkeit von 99,5 % positiv. Liegt bei einem neugeborenen Kind die Stoffwechselstörung nicht vor, so beträgt die Wahrscheinlichkeit dafür, dass das Testergebnis irrtümlich positiv ist, 0,78 %. Bei einem zufällig ausgewählten neugeborenen Kind wird der Test durchgeführt.
Betrachtet werden folgende Ereignisse:
S: „Die Stoffwechselstörung liegt vor.“
T: „Das Testergebnis ist positiv.“
a) Beschreiben Sie das Ereignis 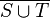 im Sachzusammenhang.
im Sachzusammenhang.
b) Berechnen Sie die Wahrscheinlichkeiten P(T) und PT(S). Interpretieren Sie das Ergebnis für PT(S) im Sachzusammenhang. (zur Kontrolle: P(T)=0,85%, PT(S)≈0,1)
ausführliche Lösung
Aufgabe 4: Abitur 2013 - 2
Quelle: ISB
In einer Großstadt steht die Wahl des Oberbürgermeisters bevor. 12 % der Wahlberechtigten sind Jungwähler, d.h. Personen im Alter von 18 bis 24 Jahren. Vor Beginn des Wahlkampfs wird eine repräsentative Umfrage unter den Wahlberechtigten durchgeführt. Der Umfrage zufolge haben sich 44 % der befragten Wahlberechtigten bereits für einen Kandidaten entschieden. Jeder Siebte derjenigen Befragten, die sich noch nicht für einen Kandidaten entschieden haben, ist Jungwähler.
Betrachtet werden folgende Ereignisse:
J: „Eine aus den Befragten zufällig ausgewählte Person ist Jungwähler.“
K: „Eine aus den Befragten zufällig ausgewählte Person hat sich bereits für einen Kandidaten entschieden.“
a) Erstellen Sie zu dem beschriebenen Sachzusammenhang eine vollständig ausgefüllte Vierfeldertafel.
b) Zeigen Sie, dass 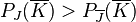 gilt.
Begründen Sie, dass es trotz der Gültigkeit dieser Ungleichung nicht sinnvoll ist, sich im Wahlkampf vo
rwiegend auf die Jungwähler zu konzentrieren.
gilt.
Begründen Sie, dass es trotz der Gültigkeit dieser Ungleichung nicht sinnvoll ist, sich im Wahlkampf vo
rwiegend auf die Jungwähler zu konzentrieren.
c) Der Kandidat der Partei A spricht an einem Tag während seines Wahlkampfs 48 zufällig ausgewählte Wahlberechtigte an. Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich darunter genau sechs Jungwähler befinden.
ausführliche Lösung
Aufgabe 5: Abitur 2012 - 1
Quelle: ISB
Für eine Aufgabe aus dem Fachgebiet Mathematik kommen zwei Kuverts zum Einsatz, die jeweils fünf Spielkarten enthalten. Es ist bekannt, dass das eine Kuvert genau zwei und das andere genau drei rote Spielkarten enthält. Der Showmaster wählt, jeweils zufällig, ein Kuvert und aus diesem zwei Karten aus.
e) Bestätigen Sie rechnerisch, dass die Wahrscheinlichkeit dafür, dass die beiden ausgewählten Karten rot sind, 20 % beträgt.
f) Der Showmaster zeigt die beiden ausgewählten Karten; sie sind tatsächlich rot. Der Kandidat wird nach der Wahrscheinlichkeit dafür gefragt, dass die beiden Karten aus dem Kuvert mit den drei roten Karten stammen. Bestimmen Sie diese Wahrscheinlichkeit.
ausführliche Lösung
Aufgabe 6: Abitur 2012 - 2
Quelle: ISB
Nachdem die Verfilmung eines bekannten Romans erfolgreich in den Kinos gezeigt wurde, veröffentlicht eine Tageszeitung das Ergebnis einer repräsentativen Umfrage unter Jugendlichen. Der Umfrage zufolge hatten 88 % der befragten Jugendlichen den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen, 18 % sahen die Verfilmung. Von den Befragten, die laut Umfrage den Roman zum Zeitpunkt des Kinostarts bereits gelesen hatten, gaben 60 % an, die Verfilmung gesehen zu haben.
Betrachtet werden folgende Ereignisse:
R: „Eine aus den Befragten zufällig ausgewählte Person hatte laut Umfrage den Roman zum Zeitpunkt des Kinostarts bereits gelesen.“
V: „Eine aus den Befragten zufällig ausgewählte Person sah laut Umfrage die Verfilmung.“
a) Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine aus den Befragten zufällig ausgewählte Person, die laut Umfrage den Roman zum Zeitpunkt des Kinostarts noch nicht gelesen hatte, angab, die Verfilmung gesehen zu haben.
b) Beschreiben Sie das Ereignis 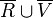 im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses.
im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses.
ausführliche Lösung
Aufgabe 7: Abitur 2011 - 1
Quelle: ISB
Ein Investor plant, in einer Gemeinde, die aus den Orten Oberberg und Niederberg besteht, eine Windkraftanlage zu errichten. Um sich einen Überblick darüber zu verschaffen, wie die Einwohner zu diesem Vorhaben stehen, beschließt der Gemeinderat, eine Umfrage unter den Wahlberechtigten der Gemeinde durchzuführen. In Niederberg werden 1722, in Oberberg 258 Einwohner befragt. 1089 aller Befragten äußern keine Einwände gegen die Windkraftanlage, darunter sind allerdings nur 27 Einwohner von Oberberg. Die übrigen befragten Personen sprechen sich gegen die Windkraftanlage aus.
a) Bestimmen Sie jeweils den prozentualen Anteil der Gegner der Windkraftanlage unter den Befragten von Niederberg und unter den Befragten von Oberberg.
Aus allen Befragten wird zufällig eine Person ausgewählt.
b) Ermitteln Sie
- die Wahrscheinlichkeit p1 dafür, dass die ausgewählte Person in Oberberg wohnt und sich gegen die Windkraftanlage aussprach.
- die Wahrscheinlichkeit p2 dafür, dass die ausgewählte Person in Oberberg wohnt, wenn bekannt ist, dass sie sich gegen die Windkraftanlage aussprach.
c) Begründen Sie, dass kein Ergebnis der Umfrage denkbar ist, bei dem p1 > p2 ist.
ausführliche Lösung
Aufgabe 8: Abitur 2011 - 2
Quelle: ISB
Bei einer Routineinspektion wird die Passagierkabine eines zufällig ausgewählten Flugzeugs des Typs X überprüft. Ein Mangel der Beleuchtung so wie ein Mangel der Klimaanlage liegen bei Flugzeugen dieses Typs jeweils mit einer bestimmten Wahrscheinlichkeit vor; diese Wahrscheinlichkeiten können der folgenden Vierfeldertafel entnommen werden.
|
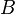 : Beleuchtung einwandfrei : Beleuchtung einwandfrei
|
a) Bestimmen Sie den Wert von x und beschreiben Sie das zugehörige Ereignis in Worten.
b) Mit welcher Wahrscheinlichkeit liegt bei dem zufällig ausgewählten Flugzeug des Typs X ein Mangel der Klimaanlage vor, wenn die Beleuchtung nicht einwandfrei funktioniert?
c) Bei Flugzeugen eines anderen Typs Y liegt ein Mangel der Klimaanlage mit einer Wahrscheinlichkeit von 4 % vor. Die Wahrscheinlichkeit dafür, dass mindestens einer der beiden Mängel vorliegt, beträgt 5 %. Wenn mindestens einer der beiden Mängel vorliegt, so funktioniert mit einer Wahrscheinlichkeit von 40 % die Beleuchtung nicht einwandfrei. Stellen Sie zu der für Flugzeuge des Typs Y beschriebenen Situation eine vollständig ausgefüllte Vierfeldertafel auf.
ausführliche Lösung
Aufgabe 9: Musterabitur 2011
ausführliche Lösung
Aufgabe 10: Aufgabe aus länderübergreifendem Aufgabenpool
Quelle: ISB
Bei der Produktion von Halbleiterbauteilen eines bestimmten Typs ist im Mittel jedes fünfte Bauteil fehlerhaft. Jedes produzierte Bauteil wird abschließend einer Kontrolle unterzogen und dabei entweder als fehlerhaft oder als einwandfrei eingestuft. Im Rahmen der Kontrolle wird ein fehlerhaftes Bauteil mit einer Wahrscheinlichkeit von 90 % als fehlerhaft eingestuft. Die Wahrscheinlichkeit dafür, dass ein einwandfreies Bauteil als fehlerhaft eingestuft wird, beträgt 40 %.
a) Bestimmen Sie die Wahrscheinlichkeit dafür, dass ein nach der Kontrolle zufällig ausgewähltes Bauteil einwandfrei ist und im Rahmen der Kontrolle korrekt eingestuft wurde.
b) Ermitteln Sie die Wahrscheinlichkeit dafür, dass ein nach der Kontrolle zufällig ausgewähltes Bauteil fehlerhaft ist, wenn es im Rahmen der Kontrolle als einwandfrei eingestuft wurde.
ausführliche Lösung
Aufgabe 11: Übungsklausur
ausführliche Lösung
Aufgabe 12: Übungsklausur - Nachschrift
ausführliche Lösung