Bitte Link zu den Originalaufgaben ausbessern und Gesamtlösung hochladen
- Aufgabe 1
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft.
3 BE
- [Lösung anzeigen][Lösung ausblenden]
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau.
6 BE
- [Lösung anzeigen][Lösung ausblenden]
c) Berechnen Sie die Koordinaten des Schnittpunkts Sa von ga mit H.
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ]
3 BE
- [Lösung anzeigen][Lösung ausblenden]
d) Zeigen Sie, dass der Punkt S (-2 / 6 / 4) derjenige Punkt aus der Schar der Schnittpunkte Sa ist, der die geringste Entfernung vom Ursprung hat. Geben Sie diese Entfernung an.
9 BE
- [Lösung anzeigen][Lösung ausblenden]
e) Die Punkte Sa bilden in H eine Kurve. Diese wird parallel zur
x3-Achse in die x1x2-Ebene projiziert; die Projektion heißt P.
Fertigen Sie eine Zeichnung von P in der x1x3-Ebene an. Um welchen Kurventyp handelt es sich bei P vermutlich? Überprüfen Sie Ihre Vermutung, indem Sie eine Koordinatengleichung von P aufstellen.
8 BE
- [Lösung anzeigen][Lösung ausblenden]
|
- Aufgabe 2
Ferner sind die Punkte A ( 1 / 6 / 1) und B (-2 / 9 / 1) gegeben.
a) Weisen Sie nach, dass sich die Punkte A und B zu einem regulären Sechseck ABCDEF mit dem Mittelpunkt S (-2 / 6 / 4) ergänzen lassen.
Ermitteln Sie die Koordinaten der Ergänzungspunkte C und D.
5 BE
- [Lösung anzeigen][Lösung ausblenden]
b) Das Sechseck ABCDEF rotiert nun um die Achse AD.Beschreiben Sie das Aussehen des dabei entstehenden Rotationskörpers. Ermitteln Sie eine Gleichung der kleinsten Kugel, die den Rotationskörper enthält.
Liegt der Ursprung des Koordinatensystems innerhalb oder außerhalb dieses Rotationskörpers? Begründen Sie Ihre Antwort.
6 BE
- [Lösung anzeigen][Lösung ausblenden]
|
 3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 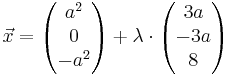 ,
, 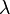 ∈
∈ 
