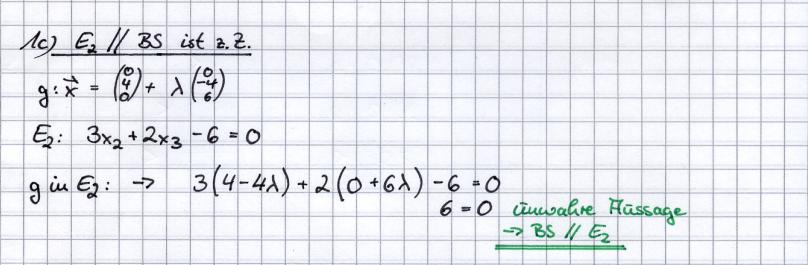|
In einem kartesischen Koordinatensystem des R3 sind die Punkte 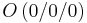 , , 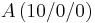 , , 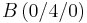 , , 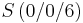 sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t  R gegeben. Die Punkte A, B und S legen die Ebene F fest. R gegeben. Die Punkte A, B und S legen die Ebene F fest.
- Aufgabe 1
- a) Bestimmen Sie eine Gleichung der Ebene F in Normalenform.
3 BE
- [mögliches Ergebnis: 6x1 + 15x2 + 10x3 - 60 = 0]
- [Lösung anzeigen][Lösung ausblenden]
- b) Berechnen Sie, unter welchem Winkel die Ebene F die x1x2 - Ebene schneidet.
3 BE
- [Lösung anzeigen][Lösung ausblenden]
- c) Zeigen Sie, dass die Ebene E2 parallel zur Geraden BS ist.
3 BE
- [Lösung anzeigen][Lösung ausblenden]
- d) Zeigen Sie, dass die zu AO parallele Mittelparallele des Dreiecks AOS identisch ist mit der Geraden p, die alle Ebenen der Schar Et gemeinsam haben.
5 BE
- [Lösung anzeigen][Lösung ausblenden]
|
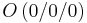 ,
, 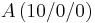 ,
, 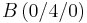 ,
, 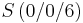 sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t
sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t  R gegeben. Die Punkte A, B und S legen die Ebene F fest.
R gegeben. Die Punkte A, B und S legen die Ebene F fest.