2005 VI
|
|
|
In einem kartesischen Koordinatensystem ist die Geradenschar
ga : |
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform. [mögliches Ergebnis E: x1 + 2x2 + 2x3 - 10 = 0] 3 BE
3 BE
4 BE
|
a) Der Punkt C wird an der Geraden AB gespiegelt. Ermitteln Sie die Koordinaten des Spiegelpunkts C*. [Ergebnis: C* = (4/8/-5)] 5 BE
4 BE
6 BE
|
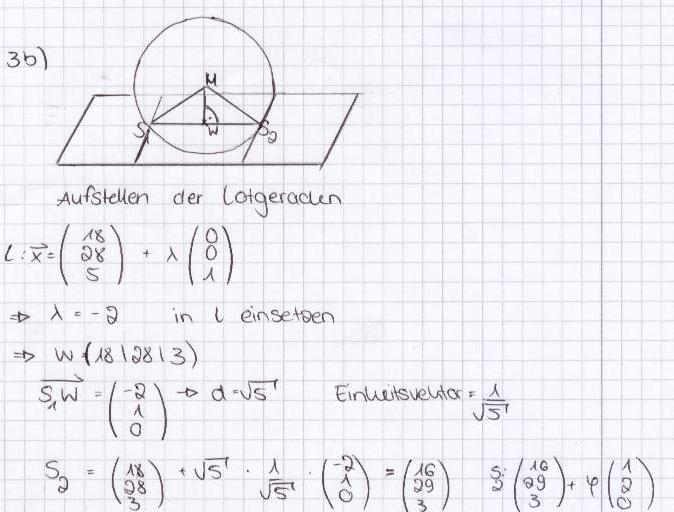
In der Ebene H: x3 = 3 liegen zwei parallele Schienen s1 und s2.Die Schiene s1 wird durch die Gerade s1 : a) Berechnen Sie die Koordinaten des Punkts S, in dem die Kugel die Schiene s1 berührt. [Ergebnis: S = (20/27/3)] 6 BE
5 BE
4 BE
|
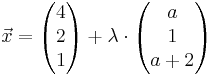 mit a,
mit a, 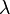

 - gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.
- gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.




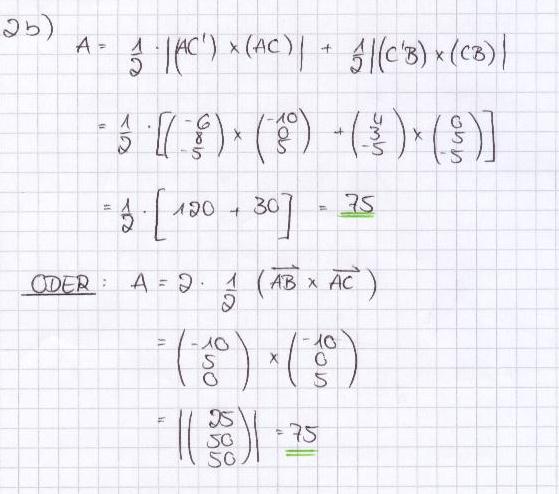

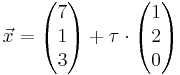 mit
mit