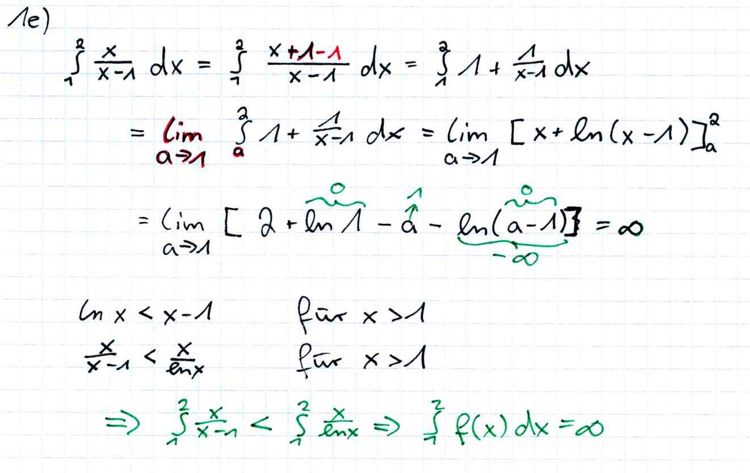2007 II
Aus RMG-Wiki
< LK Mathematik | Abitur
Version vom 18. Februar 2010, 19:56 Uhr von Stich Philipp (Diskussion | Beiträge)
|
|
1. Gegeben ist die Funktion
b) Bestimmen Sie das Monotonieverhalten von f sowie Art und Lage des Extrempunktes E von Gf .
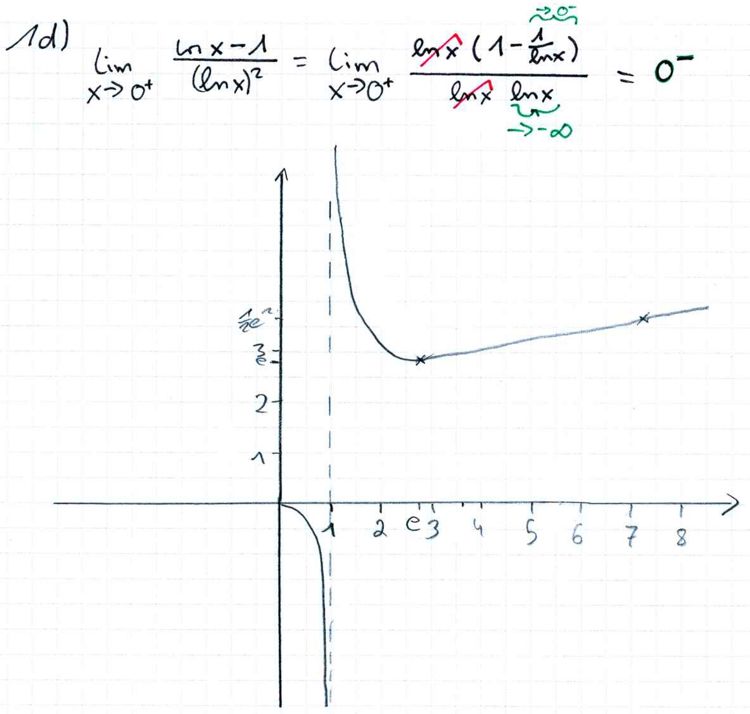
[Zur Kontrolle: c) Zeigen Sie, dass Gf einen Wendepunkt W besitzt, und berechnen Sie dessen Koordinaten. d) Berechnen Sie und skizzieren Sie Gf unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem. e) Zeigen Sie: Was folgt für ? Begründen Sie Ihre Antwort. Dabei dürfen Sie ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1. |
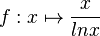 mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.

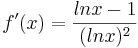 ]
]