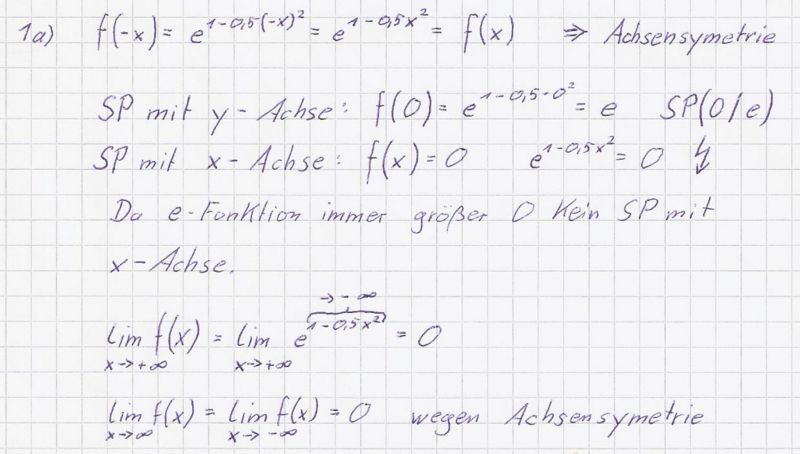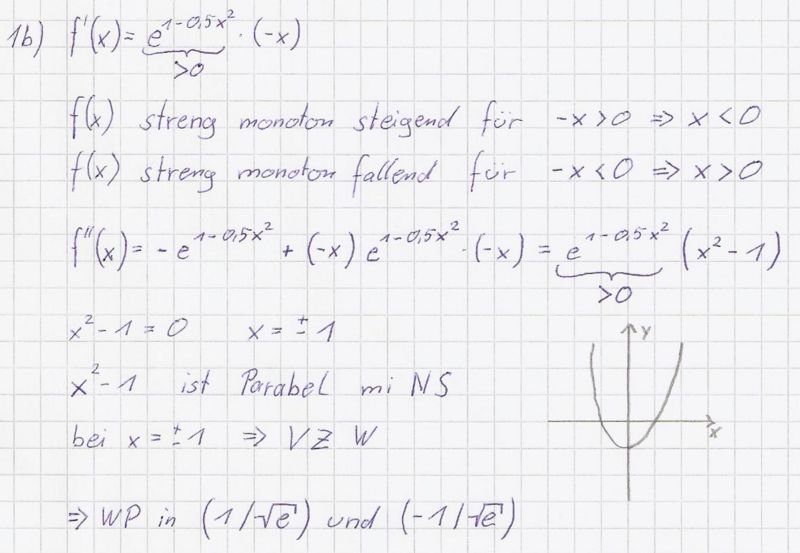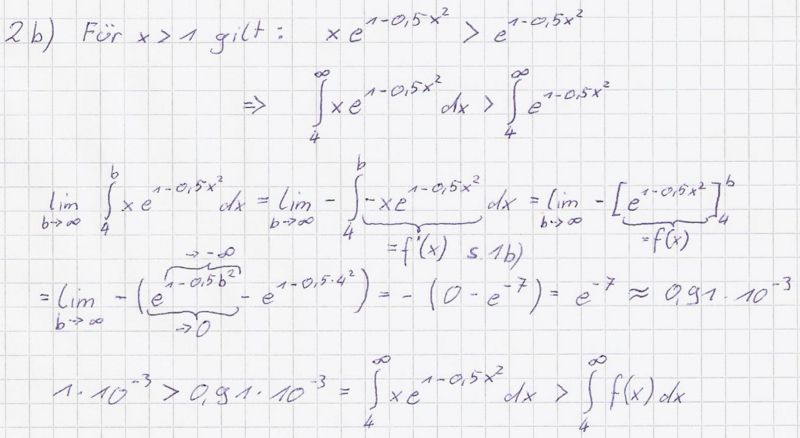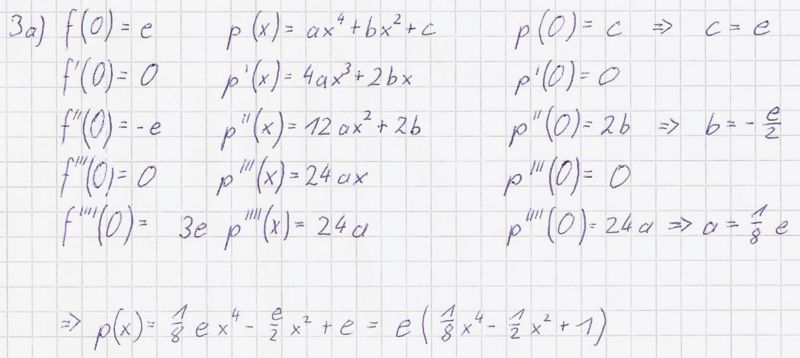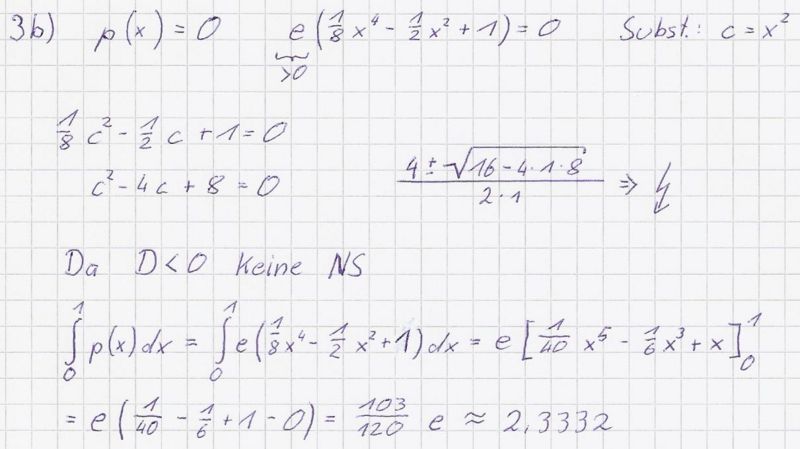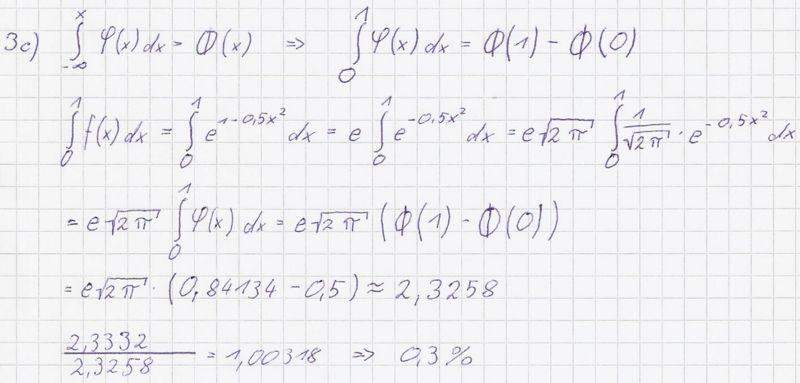2008 II
Erstellt von Alistair Mainka und Benjamin Schleicher.
Aufgabe 1
Gegeben ist die Funktion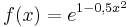 
mit Definitionsbereich Df = IR .
Die Abbildung auf der folgenden Seite zeigt den Graphen Gf von f.
a) Untersuchen Sie Gf rechnerisch auf Symmetrie und Schnittpunkte mit
den Achsen. Bestimmen Sie das Verhalten von f für x → + ∞ und x → − ∞. (4BE)
b) Zeigen Sie, dass gilt:
.
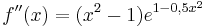Bestimmen Sie durch Rechnung das Monotonieverhalten von f und die
Koordinaten der Wendepunkte. (6BE)
Aufgabe 2
Die Integralfunktion F ist definiert durch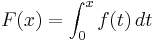 
, x ∈ IR.
a) Untersuchen Sie das Symmetrie-, Monotonie- und Krümmungsverhalten
des Graphen von F. Bestimmen Sie aus der Abbildung mit Hilfe des
Gitternetzes Näherungswerte für F(0,5), F(1), F(2) und F(4). Tragen Sie
den Graphen von F im Bereich x ∈[−4;4] in die gegebene Abbildung
ein. (8BE)
b) Für x > 1 gilt offensichtlich
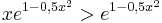. Zeigen Sie damit,
dass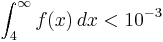 
ist.
Was folgt für die Funktionswerte von F für x ≥ 4? (5BE)
3. Die Funktion f soll im Folgenden in einer Umgebung von x = 0 durch eine
Polynomfunktion p mit dem Term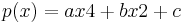 
, a, b, c ∈ IR ,
angenähert werden.
a) Bestimmen Sie die Koeffizienten a, b und c so, dass f und p an der
Stelle x = 0 im Funktionswert und in den Werten der 1. bis einschließlich
4. Ableitung übereinstimmen.
Ohne Nachweis darf verwendet werden: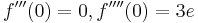 
(6BE)
[Zur Kontrolle: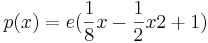 
]
b) Zeigen Sie, dass p keine Nullstelle besitzt. Berechnen Sie den Inhalt A
der Fläche, die von den Koordinatenachsen, dem Graphen von p und der
Geraden x = 1 eingeschlossen wird, auf 4 Dezimalen gerundet. (5BE)
[Zur Kontrolle: A ≈ 2,3332]
c) Bestimmen Sie nun den Wert des Integrals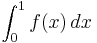 
mit Hilfe der
Gauß’schen ϕ-Funktion (
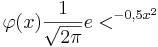) und dem stochastischen
Tafelwerk. Um wie viel Prozent weicht der Näherungswert aus
Teilaufgabe 3b von diesem Ergebnis ab? (6BE)
