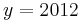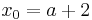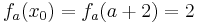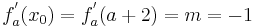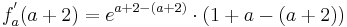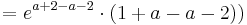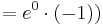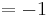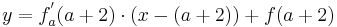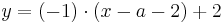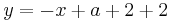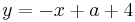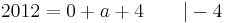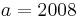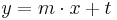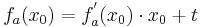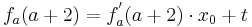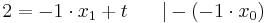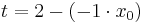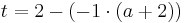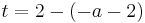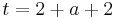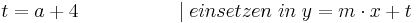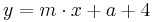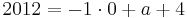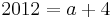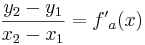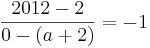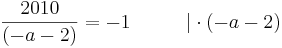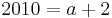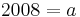Lösung von Teilaufgabe c) 1.
Aus RMG-Wiki
< Facharbeit Andre Etzel | Teilaufgabe c
Version vom 24. Januar 2010, 01:48 Uhr von Andre Etzel (Diskussion | Beiträge)
Inhaltsverzeichnis |
Tangente im Punkt Wa( a + 2 / 2 ) an Gfa mit dem Schnittpunkt A (0 / 2012 )
Lösung; Tangentengleichung
Tangentengleichung: siehe Formelsammlung Seite 58
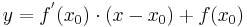
Lösung; Fußweg
Lösung; Clever