Gliederung
Aus RMG-Wiki
< Facharbeit Andre Etzel
Version vom 20. Januar 2010, 23:43 Uhr von Andre Etzel (Diskussion | Beiträge)
Für jede reelle Zahl a sei eine Funktion fa durch 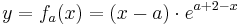 mit
mit 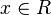 gegeben.
gegeben.
Inhaltsverzeichnis |
Teilaufgabe a)
- 1.Untersuchen Sie den Graphen von fa auf:
- Schnittpunkte mit den Koordinatenachsen,
- lokale Extrempunkte und
- Wendepunkte!
- Bestimmen Sie gegebenenfalls deren Koordinaten!
- 2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
- 3.Skizzieren Sie den Graphen der Funktion f2 für 1,6 < x <7!
Teilaufgabe b)
- 1. Geben Sie aufgrund Ihrer Ergebnisse aus Teilaufgabe a)zwei Eigenschaften des Graphen einer Stammfunktion von fa an!
- 2.Bestimmen Sie durch partielle Integration eine Gleichung einer Stammfunktion von fa!
- 3.Die x-Achse und der Graph der Funktion f2 begrenzen im I. Quadranten eine nach rechts ins Unendliche reichende Fläche. Berechnen sie deren Inhalt!
- Hinweis:
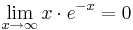
- Hinweis:
Teilaufgabe c)
- Im Punkt Wa(a+2; fa(a+2)) werde die Tangente an den Graphen von fagelegt
- 1. Für welchen Wert von a schneidet diese Tangente die y-Achse im Punkt A(0;2012)?
- Nun sei a = 2.
- 2. Berechnen Sie alle Stellen xB, für die die Tangente die y-Achse im Punkt B(xB;f2(xB)) an den Graphen von f2 durch den Koordinatenursprung verläuft!
Teilaufgabe d)
Für jeden Wert von a bilden die Punkte Ra (a / fa(a)), Ha (a+1 / fa(a+1)) und Wa (a+2 / fa(a+2)) ein Dreieck.
- 1.Zeigen Sie, dass alles diese Dreiecke zueinander kongruent sind!
- 2.Berechnen Sie deren Flächeeninhalt!
Teilaufgabe e)
Beweisen Sie, dass für die n-te Ableitung (n>1) der Funktion fa gilt:
--Andre Etzel 22:42, 20. Jan. 2010 (UTC)