Lineare Gleichungen

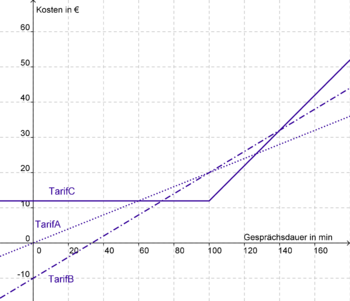
Mit linearen Gleichungen kann man eine Reihe von Problemen rechnerisch exakt lösen. Wir betrachten zur Veranschaulichung nun wieder die Handytarife der Firma "Smartphone"

Tarif A: f(x) =

Tarif B: f(x) =

Tarif C: f(x) =

Verschiedene Kunden haben folgende Probleme...

Funktionswert

Herr Müller weiß aufgrund seiner bisherigen Handyrechnungen, dass er im Monat circa 2,5 Stunden mit seinem Handy telefoniert. Da er zu einem Vertrag der Firma "Smartphone" wechseln will, möchte er nun gerne wissen welcher der Tarife für seine Bedürfnisse am günstigsten ist.

→ Hierzu wollen wir also herausfinden, mit welchem der Tarife bei 150 Minuten die geringsten Kosten entstehen.
Wir vergleichen dazu die jeweiligen Funktionswerte, also die zu x zugehörigen y - Werte, an der Stelle x = 150.

Tarif A: f (x) = 0,2x
x-Wert einsetzen: f (150) = 0,2 * 150 = 30

→ Zur 150. Gesprächsminute liegen die Kosten bei Tarif A bei 30 €.

Tarif C: f (x) =
Definitionsbereich beachten: da 150 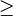$\ge$ 100, wählen wir zur Berechnung die Funktionsgleichung f (x) = 0,5x - 40
x-Wert einsetzen: f (150) = 0,5 * 150 - 40 = 35

→ Zur 150. Gesprächsminute leigen die Kosten bei Tarif A bei 35 €.

Arbeitsauftrag 1: Berechne die den Funktionswert, also die anfallenden Kosten, für x = 150 bei Tarif B!

Arbeitsauftrag 2: Vergleiche nun alle Werte und entscheide, welcher der drei Tarife für Herrn Müller am geeignetsten ist!

x-Wert

Frau Schmidt ist bereits Kundin bei "Smartphone" und nutzt im Moment Tarif B. Da sie sich entschieden hat im Monat künftig nicht mehr als 20 € an Handykosten ausgeben zu wollen, will sie überprüfen, ob eventuell einer der beiden anderen Tarife für sie bessere Konditionen bietet.

→ Um das herauszufinden überlegen wir nun, welcher der Tarife bei 30 € die meisten Gesprächsminuten zulässt.
Wir suchen also die jeweiligen x-Werte an einer bestimmten Stelle y = 20.

Tarif A: f (x) = 0,2x
y-Wert einsetzen: 20 = 0,2x (Bedenke, dass f (x), also der Funktionswert, gleichbedeutend mit y ist!)

nach x auflösen: x = 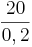$\frac{20}{0,2}$ = 100

→ Für 20 € kann Frau Schmidt bei Tarif A 100 Minuten telefonieren.

Arbeitsauftrag 1: Berechne auch die x-Werte zu den anderen beiden Tarifen!

Arbeitsauftrag 2: Welchen Tarif wird Frau Schmidt wohl wählen?

Nullstelle

Jonas entscheidet sich dafür einen Tarif ohne Grundgebühr zu wählen, weiß aber noch nicht ob Tarif A oder das Aktionsangebot Tarif B für ihn interessanter ist. Dazu möchte er erst einmal wissen wie viele kostenlose Gesprächsminuten er bei Tarif B theoretisch zur Verfügung hätte.

→ Um das herauszufinden, suchen wir nun also denjenigen Punkt, an dem sich der Graf von Tarif B und die x-Achse schneiden. Links von diesem Wert befindet sich der Graf im negativen Bereich - es fallen also keine Kosten an. Rechts davon verläuft der Graf im positiven Bereich - man muss ab dieser Minute für seine Gesprächsminuten zahlen.
Diesen Schnittpunkt des Grafen mit der x-Achse nennt man Nullstelle!

Tarif B: f (x) = 0,3x - 10
y = 0 setzen: 0 = 0,3x - 10
nach x auflösen: 10 = 0,3x; x = 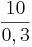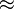$\frac{10}{0,3}$ $\approx$ 33,3

Schnittpunkt zweier Geraden

Nun möchte Jonas, um sich endgültig zu entscheiden, noch herausfinden ab welcher Gesprächsdauer Tarif B teurer wir als Tarif A.

→ Teurer ist Tarif B sobald sein Graf über dem des Tarifs A liegt, ihn also "überholt" hat. Dies geschieht ab dem Schnittpunkt der beiden Grafen.
Hier haben die Grafen den gleichen Funktionswert (die Kosten sind identisch) und den gleichen x-Wert (bei gleichr Gesprächsdauer), rechts davon sind die Funktionswerte bzw. Kosten zu Tarif B höher.

== Aufgaben==