Kehrsatz - Seite 2
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras
Version vom 25. Januar 2009, 20:09 Uhr von Zehnder Moritz (Diskussion | Beiträge)
Arbeitsauftrag:
- Setze für jedes gegebene Dreieck den Satz des Pythagoras an
- Zeichne die Dreiecke im GeoGebra Applet
- Notiere dir die Rechnungen und die Winkel aus dem GeoGebra Applet unter der Überschrift "Kehrsatz zum Satz des Pythagoras" in dein Heft
- Vergleiche die Lösung des Satzes des Pythagoras mit dem im Applet eingezeichneten Winkel!
- Was fällt dir auf?
| |
|
|
|
| |
4cm | 3cm | 5cm |
| |
4cm | 5cm | 7cm |
| |
2,1cm | 2cm | 2,9cm |
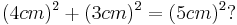
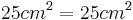
- Wahre Aussage, das heißt der Satz des Pythagoras gilt
- Aus dem Applet erkennt man, dass das Dreieck einen rechten Winkel besitzt
- Man macht den Ansatz mit a und b als Kathete und c als Hypotenuse, da c die längste Seite im Dreieck ist
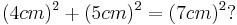
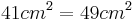
- Widerspruch, das heißt der Satz des Pythagoras gilt nicht
- Aus dem Applet erkennt man, dass das Dreieck keinen rechten Winkel besitzt
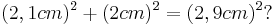
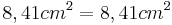
- Wahre Aussage, das heißt der Satz des Pythagoras gilt
- Aus dem Applet erkennt man, dass das Dreieck einen rechten Winkel besitzt
- Wenn der Satz des Pythagoras gilt, also über die Gleichung kein Widerspruch entsteht, besitzt das Dreieck einen rechten Winkel
- Man kann also sagen:
- Gilt für ein Dreieck der Satz des Pythagoras, so besitzt es einen rechten Winkel, der der längsten Seite gegenüberliegt
Hier geht es zum Hefteintrag

