Leere Seite

Seite noch im Aufbau!

Wiederholung: Ökologie

Zunächst zu den Grundlagen: Bei der Thematik "Ökologie" wird gelegentlich auf Wissen aus der zehnten Jahrgangsstufe zurückgegriffen. Auch im normalen Q11-Unterricht wiederhole ich diese Grundlagen nicht ausführlich, sondern verweise lediglich auf ein Skript aus der zehnten:

Skript "Ökologie" (10. Jahrgangsstufe) als pdf-Datei

Die Hefteinträge sind zwar kurz, sollten aber verständlich sein. Es geht hauptsächlich darum, dass ihr euch unter bestimmten Begriffen etwas vorstellen und diese auch bei Erklärungen sicher verwenden könnt:

• Produzenten, Konsumenten, Destruenten
• Ökosystem, Biotop, Biozönose
• Biotische und abiotische Umweltfaktoren

Es wird im Kolloquium aber sicher keine Fragen geben: "Was bedeutet Biotop?"

• Wenn ihr zu den Vitalitätskurven etwas machen möchtet, dann könnt ihr im neuen Wiki die Einheit Biologie5 und Biologie6 auf der folgenden Seite bearbeiten: [Hier klicken]. Für einige Aufgaben ist dazu zwar das Buch aus der zehnten Jahrgangsstufe nötig, aber diese Aufgaben könnt ihr überspringen.
  

• Das Konkurrenzausschlussprinzip, das stark mit dem Begriff der ökologischen Nische zusammenhängt, ist für mich aus biologischer Sicht ein äußerst spannendes Prinzip. In der zehnten Jahrgangsstufe mache ich dazu viele Beispiele. Im Kolloquium habe ich jedoch noch nie darauf Bezug genommen und habe es auch nicht vor. Falls ihr trotzdem dazu mehr wissen möchtet: Das Video von simpleclub ist ganz o.k.:
  

• Den Punkt "Populationsschwankungen" bespreche ich in der Q11 erneut (auch in der folgenden Einheit).

Neu: Populationsentwicklung
Dieser Punkt soll folgende Fragen klären:

• Welche mathematischen Grundsätze stecken hinter der zahlenmäßigen Entwicklung einer Population?
• Welche Umweltfaktoren spielen eine Rolle?
• Kann man das Fortpflanzungsverhalten von Tieren, welches eng mit der Populationsentwicklung zusammenhängt, in unterschiedlich Kategorien einteilen?

Mathematische Grundsätze: Exponentielles Wachstum
Stellt euch folgendes Beispiel vor: Vor 100 Jahren gerät ein Handelsschiff in einen Sturm, erleidet Schiffbruch und geht mitten im Meer unter. Auf dem Schiff befanden sich versteckt zwischen den Vorräten der Besatzung etliche Ratten. Nahezu alle sterben beim Sinken des Schiffes, lediglich ein Pärchen kann sich im Sturm lange genug durch die Wellen schlagen, bis es schließlich auf eine von Tieren nahezu unbewohnte Insel gespült wird. Es gibt etliche Pflanzen, die Früchte produzieren und gelegentlich nisten auch Vögel auf der Insel, von deren Eiern sich die Ratten gelegentlich welche stibitzen können. Die Ratten sind (nach einer schlimmen Odysee) letztlich in einem "Paradies" gelandet. Nehmt an, dass dieses Ratten-Paar in einem Jahr acht Jungtiere zur Welt bringt, gleich viele Männchen und Weibchen. Von dieser Familie sterben zwei Tiere (idealerweise ein Männchen und ein Weibchen) im Verlauf des Jahres z.B. weil sie zu neugierig waren. Nach einem Jahr befinden sich folglich acht Tiere auf der Insel.

• Berechnet, wie viele Tiere sich nach zwei, drei, vier, fünf und sechs Jahren auf der Insel befinden, wenn sich an den Bedingungen (jeweils 8 - 2 Tiere Nachwuchs pro Paar ) ändert!
• Zeichnet eine Grafik (oder lasst Excel eine Grafik zeichnen), die die Anzahl der Tiere (die "Populationsgröße") auf der Insel in Abhängigkeit von der Zeit zeigt!

[Anzeigen][Verstecken]

Es kann sein, dass ihr zu anderen Zahlenwerten gekommen seid. Entscheidend ist die Form der Kurve: Sie zeigt ein typisch exponentielles Wachstum: Je länger der betrachtete Zeitraum ist, desto schneller steigt die Anzahl der Tiere. Die Mathematik zur Beschreibung dieser Kurve ist nicht trivial und soll hier an dieser Stelle keine große Rolle spielen. Entscheidend ist, dass ihr erkennt, welche Parameter Einfluss auf den Verlauf der Kurve haben: Die Anzahl der Ausgangsindividuen N₀, die Geburtenrate (b) (birth), die Sterberate (d) (death) und die Zeit (t). Aus der Geburten- und Sterberate lässt sich die sogenannte Zuwachsrate (r) bestimmen. Diese Größe wird später noch einmal eine wichtige Rolle spielen.

Mathematische Grundsätze: Logistisches Wachstum
Selbstverständlich kann die vorher gezeichnete Kurve nicht allgemein gelten. Bleiben wir beim Beispiel mit den Ratten auf einer einsamen Insel: Innerhalb weniger Jahre wäre die gesamte Oberfläche der Insel mit Ratten komplett bedeckt. Dieser Zustand wird nie erreicht. Grund dafür sind sogenannte dichteabhängige Faktoren, die dafür Sorgen, dass bei einer hohen Dichte an Tieren die Geburtenraten zurückgeht bzw. die Sterberate steigt, auf jeden Fall also die Wachstumsrate (r) sinkt.
Überlege selbst, welche Faktoren das sein könnten und wie (über welche Mechanismen) diese Faktoren die Geburtenrate bzw. die Sterberate beeinflussen!

[Anzeigen][Verstecken]

• Verfügbarkeit von Ressourcen: Wenn viele Ratten vorhanden sind, gibt es für jede einzelne Ratte weniger (z.B.) zu Fressen. Im einfachsten Fall könnten Tiere verhungern (d steigt). Es könnte aber auch sein, dass die Tiere versuchen, andere Sachen zu fressen und sich dabei vergiften (d steigt). Oder sie finden einfach sehr wenig zu fressen, die Weibchen gebären keine oder nur noch weniger Jungtiere (b sinkt) bzw. sie sind nicht in der Lage ihre Jungtiere mit genügend Milch zu versorgen und etliche sterben (d steigt).
• Stress-Level steigt: Vor allem Tieren, die ein Revier ausbilden, ist der Aufwand zum Verteidigen des Reviers größer, wenn es viele Tiere (also Rivalen, Konkurrenten) gibt. Untersuchungen belegen, dass Stress die Sterberate erhöht. Die genauen Mechanismen sind vielfältig, z.B. führt eine andauernd starke Belastung des Herz-Kreislaufsystems zu Herzinfarkt.
• Parasiten und Krankheitserreger: Wenn viele Tiere eng zusammenleben, ist es für Parasiten und Krankheitserreger leichter sich zu verbreiten. Weil die Kontakthäufigkeit von befallenen/infizierten Tieren mit nicht befallenen/infizierten steigt. Das kann die Sterberate erhöhen, bzw. die Geburtenrate senken, wenn der Körper des schwangeren oder säugenden Weibchens ausgezehrt ist.

Zusammengefasst bedeutet das: In unserem theoretischen Beispiel von schiffbrüchigen Ratten würden nach einer exponentiellen Vermehrungsphase nach und nach dichteabhängige Faktoren immer stärker wirken, die dazu führen, dass die Wachstumsrate immer stärker sinkt. Im theoretischen Idealfall nähert sich die Anzahl der Tiere einem Grenzwert an, bei dem genauso viele Tiere sterben, wie neu geboren werden. Die Anzahl der Tiere in einem bestimmten Gebiet ändert sich dann nicht mehr. Diese Anzahl an Tieren, die in einem bestimmten Gebiet dauerhaft stabil überleben kann, nennt man Umweltkapazität K.
Überführt man diese Überlegungen in die Grafik von einem typischen Populationswachstum, ergibt sich das folgende Bild, dessen Verlauf als logistisches Wachstum bezeichnet wird:

Wiederholung
Diese Kurve sollte euch nicht neu sein. Bereits in der 8. Klasse taucht diese Kurve beim Wachstum von Bakterien auf. Bakterien vermehren sich durch Zweiteilung, die Anzahl verdoppelt sich also immer nach einem bestimmten Zeitintervall (z.B. 20 min.). Vielleicht habt ihr schon einmal Joghurt hergestellt: Man gibt einen Löffel reinen Joghurt (der Milchsäure-Bakterien enthält) in ein Glas Milch und stellt das über Nacht an einen warmen Ort. Am nächsten Tag ist aus der Milch Joghurt geworden. Im Prinzip haben sich die Bakterien exponentiell vermehrt, dabei Milchsäure hergestellt und diese wiederum lässt das Eiweiß in der Milch gerinnen. Man erhält eine feste Masse: Joghurt.

[Anzeigen][Verstecken]

BLA1 BLA1 BLA1

Realistisches Wachstum
Betrachtet man das Populationswachstum von größeren Tieren, so stellt man nahezu immer fest, dass sich kein mathematisch perfektes, logistisches Wachstum ergibt. Sehr häufig schwankt die Anzahl der Tiere um die Umweltkapazität K. Auch dafür sind die Gründe vielfältig. Zunächst soll hier wieder ein sehr einfaches Beispiel herangezogen werden: Bleiben wir bei den schiffbrüchigen Ratten. Nehmen wir an, die Umweltkapazität auf der Insel beträgt 10.000 Tiere. Viele Jahre lang leben tatsächlich ungefähr so viele Tiere auf der Insel. In einem Jahr bricht die Zahl plötzlich stark ein. Stellt eine Hypothese auf, welcher Faktor für einen solchen Rückgang verantwortlich sein könnte. Bedingung: Es darf kein dichteabhängiger Faktor sein, der bereits besprochen wurde (also z.B. der Ausbruch einer Seuche o.ä.)!

[Anzeigen][Verstecken]

Zum Beispiel könnte ein später Wintereinbruch die Blüte einer wichtigen Futterpflanze gestört haben, wodurch es in einem Jahr viel weniger Früchte als üblich gibt. Solche Faktoren, die mit der Dichte der Population nichts zu tun haben (oft handelt es sich um abiotische Umweltfaktoren), nennt man dichteunabhängige Faktoren. Sie beeinflussen eher die Umweltkapazität K.

• Überlegt euch weitere solche Szenarien mit dichteunabhängigen Faktoren!

[Anzeigen][Verstecken]

• Regenmenge: Beeinflusst Wachstum von Gras/Pflanzen, was von vielen Tieren als Nahrung genutzt wird.
• Temperatur: Mehr oder weniger Frost hat oft massive Auswirkungen auf das Leben in einem Gebiet
• Nährstoffeintrag: Zum Beispiel durch Überflutungen oder Phänomene wie El Nino können Landstriche oder Meeresgebiet plötzlich viel mehr oder weniger Lebewesen mit Nahrung versorgen

(Um euch nicht zu enttäuschen: Das Vorschau-Bild vermittelt einen völlig falschen Eindruck vom Video. Es werden keine Menschen darin zu sehen sein!)

[Anzeigen][Verstecken]

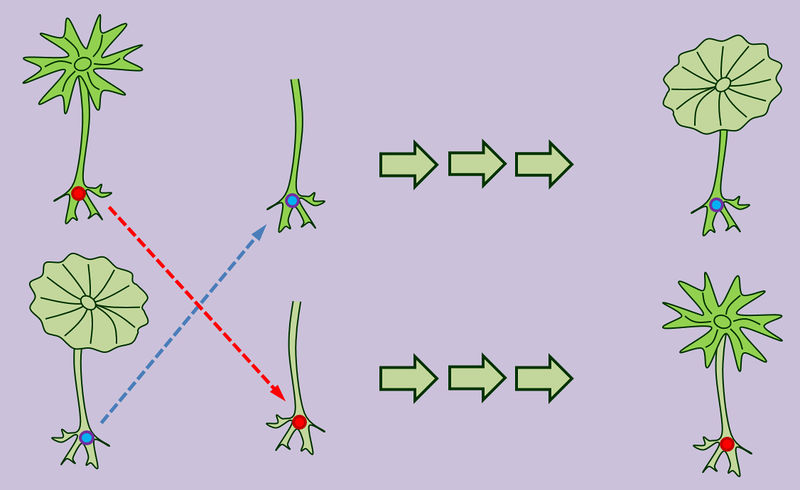
• Versuchsaufbau: Man verwendet verschiedene Arten von Acetabularia. Das sind einzellige Grünalgen, die sich vor allem in der Form ihres Hutes unterscheiden. Eine typische Eigenschaft dieser Algen ist das Nachwachsen des Hutes, wenn man ihn abschneidet. die Hüte zweier verschiedener Acetabularia-Arten wurden entfernt und die Zellkerne, die im Rhizoid sitzen vertauscht.
• Ergebnis: Es wächst (nach einigen Zwischenformen) die Hut-Form, die zum transplantierten Zellkern passt.
• Schlussfolgerung: Der Zellkern enthält die Informationen über die Merkmale der Zelle.