Abi 2014 Analysis I Teil B
|
|
|
Gegeben ist die Funktion
a) Berechnen Sie die Koordinaten der Schnittpunkte von Gf mit den Koordinatenachsen. Bestimmen Sie das Verhalten von f für x→-∞ und geben Sie f(6) an. b) Bestimmen Sie den Term der Ableitungsfunktion f' von f und geben Sie die maximale Definitionsmenge von f´ an. Bestimmen Sie (zur Kontrolle: c) Geben Sie das Monotonieverhalten von Gf und die Wertemenge von f an. d) Geben Sie f(-2) an und zeichnen Sie Gf unter Berücksichtigung der bisherigen Ergebnisse in ein Koordinatensystem ein (Platzbedarf im Hinblick auf die folgenden Aufgaben: -3 ≤ y ≤ 7 ). e) Die Funktion f ist in Df umkehrbar. Geben Sie die Definitionsmenge der Umkehrfunktion f-1 von f an und zeigen Sie, dass
|
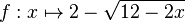 mit maximaler Definitionsmenge
Df = ]-∞;6]. Der Graph von f wird mit Gf bezeichnet.
mit maximaler Definitionsmenge
Df = ]-∞;6]. Der Graph von f wird mit Gf bezeichnet.
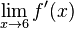 und beschreiben Sie, welche Eigenschaft von Gf aus diesem Ergebnis folgt.
und beschreiben Sie, welche Eigenschaft von Gf aus diesem Ergebnis folgt.
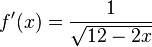 )
)
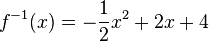 gilt.
gilt.

