Lineare Gleichungen
Aus RMG-Wiki
< Digitaler Lernpfad zu linearen Funktionen | Inhaltsverzeichnis
Version vom 18. November 2009, 15:50 Uhr von Köhler Lisa (Diskussion | Beiträge)
Inhaltsverzeichnis |
Punkt - Gerade
Nullstellen
Ein Vertragskunde entscheidet sich dafür einen Tarif ohne Grundgebühr zu wählen, weiß aber noch nicht ob Tarif A oder das Aktionsangebot Tarif B für ihn interessanter ist. Dazu möchte er erst einmal wissen wie viele kostenlose Gesprächsminuten er bei Tarif B theoretisch zur Verfügung hätte.
→ Um das herauszufinden, suchen wir nun also denjenigen Punkt, an dem sich der Graf von Tarif B und die x-Achse schneiden. Links von diesem Wert befindet sich der Graf im negativen Bereich - es fallen also keine Kosten an. Rechts davon verläuft der Graf im positiven Bereich - man muss ab dieser Minute für seine Gesprächsminuten zahlen.
Diesen Schnittpunkt des Grafen mit der x-Achse nennt man Nullstelle!
Rechenverfahren
y-Abschnitt
Anwendung
Rechenverfahren
Steigung
Schnittpunkt zweier Geraden
Anwendung
Rechenverfahren
Aufgaben
- Lies aus den folgenden Geradengleichungen sowohl die Steigung als auch den y-Abschnitt ab!
- a) y = 2x - 4
- b) y =
 x + 2
x + 2
- c) y = -
 x + 1
x + 1
- d) y = 3x - 0,5
- Zeichen die Grafen der folgenden Geraden!
- a) y = -x
- b) y = 0,5
- c) y = -2
- d) y =
 x - 1
x - 1
- e) y = -1,5x + 2
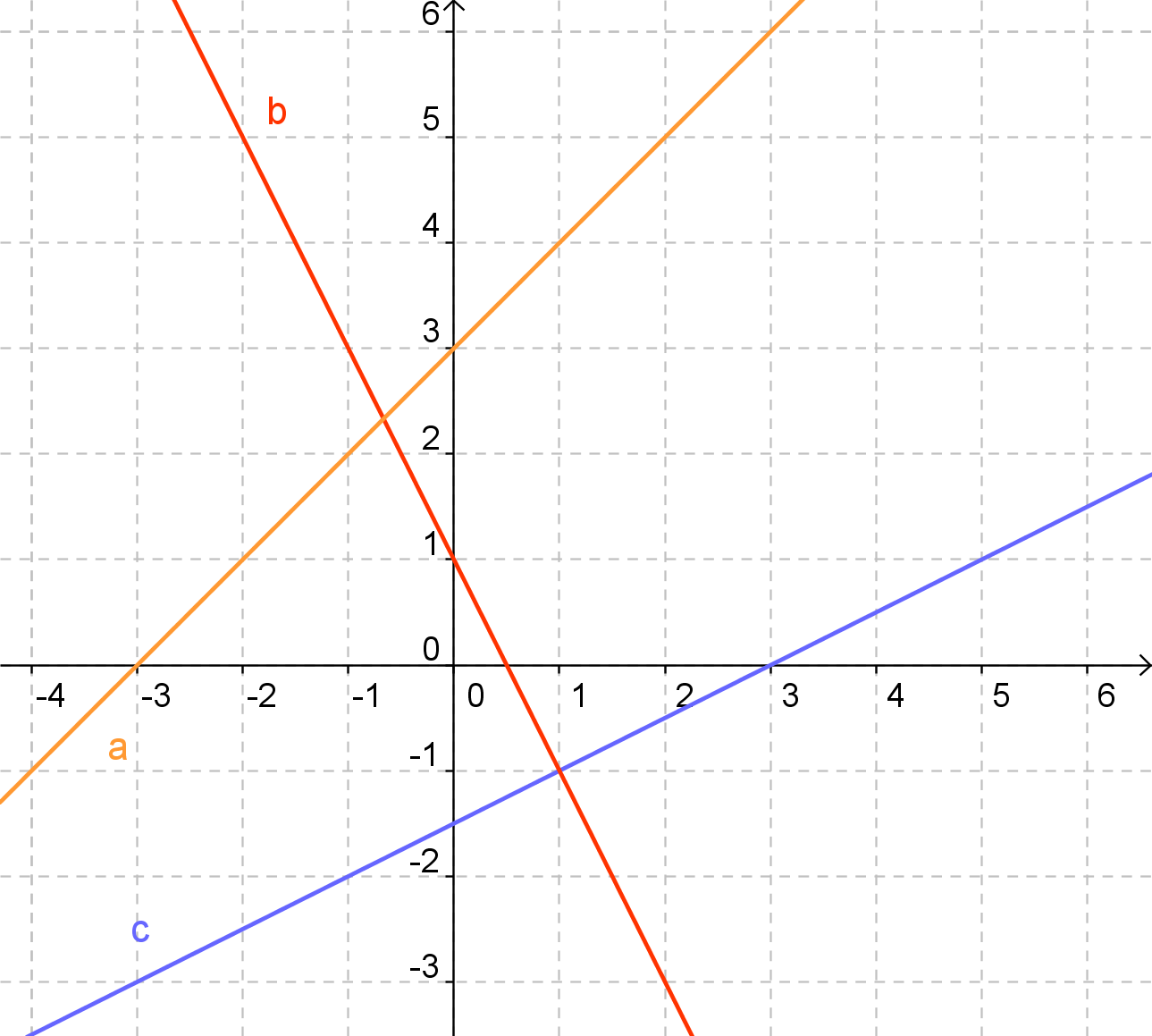
- Ordne den dargestellten Geraden jeweils eine Geradengleichung zu!
- Sind die folgenden Funktionen linear? Begründe jeweils deine Entscheidung!
- a) f(x) = 23 - 15x
- b) f(x) = 2x² - 4
- c) f(x) = 3x + 0,5x
- Gib zu den in Worten genannten Vorschriften jeweils eine Funktionsgleichung an!
- a) Jedem x wird das Doppelte zugeordnet.
- b) Jedem x wird das um 3 verminderte Vierfache zugeordnet.
- c) Jedem x wird das um 2 verminderte Dreifache zugeordnet.
- Zeichne die Grafen der beiden abschnittsweise defienierten Funktionen!
- a)