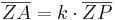Zentrische Streckung
Die Zentrische Streckung
|
Bei der bisher behandelten Abbildungen, wie Achsenspiegelung, Drehung, Verschiebung, die unter dem Namen Kongruenzabbildungen zusammengefasst werden, blieb die Größe unverändert. |
|
Merke:
|
Eigenschaften der Zentrischen Streckung:
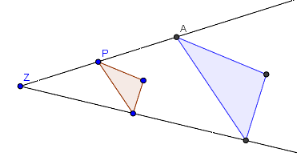
- Die Zentrische Streckung ist eine geradentreue Abbildung. Jede Gerade, die nicht durch das Streckzentrum verläuft wird auf eine zu ihr parallele Bildgerade abgebildet. z.B.
- Die Zentrische Streckung ist verhältnistreu. Jede Urstrecke wird auf eine parallele Bildstrecke der k - fachen Länge abgebildet. z.B.
- Die Zentrische Streckung ist eine winkeltreue Abbildung. Jeder Winkel wird auf einen gleich großen Winkel abgebildet. z.B.
- Die Bildfigur hat den k2 - fachen Flächeninhalt der Originalfigur. z.B.
Die nachfolgende Abbildung zeigt die Zentrische Streckung eines Fünfeckes. Mit Hilfe der Maus kannst du die Punkte verschieben.
Arbeitsauftrag:
Zeichne den Stadtplan unter der Überschrift "Die Zentrische Streckung" verkleinert in dein Heft und schreibe die Merksätze daneben.