Benutzer:Köhler Lisa
Aus RMG-Wiki
Version vom 29. September 2008, 14:22 Uhr von Köhler Lisa (Diskussion | Beiträge)
Hausaufgabe vom 25.08.2008 AB Infinitesimalrechnung; S.216/10
Aufgabenstellung: Wie groß ist die Fläche, die vom Graphen Gf der Funktion f(x)=-1/3x2+2x+1, der Ordinate des höchsten Punktes, der x-Achse und der y-Achse eingeschlossen wird?
1) Berechnung des Maximums: f´(x)=0; -2/3x+2=0; x=3; Maximum (3/4)
2) Flächenberechnung:
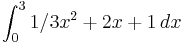 = 9
= 9
Hausaufgabe vom 23.09.2008 S.211/7
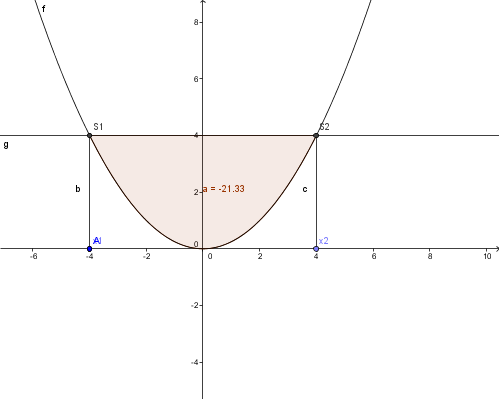
Aufgabenstellung: Berechne den Inhalt des Segments, das die Gerade mit der Gleichung y-4=0 vom Graphen der Funktion 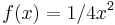 abschneidet!
abschneidet!
Lösung
1. Schnittstellen berechnen: x1 = -4 ; x2 = 4
2. A = 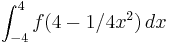 =
= ![\left[ 4x-1/4 (x^3)/3\right]](/images/math/c/1/3/c135c5292b953852b50b3ed9c66e6466.png) = ... = 64/3
= ... = 64/3