Abi 2015 Analysis II Teil B
|
|
Gegeben ist die Funktion f mit a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
b) Begründen Sie, dass die x-Achse horizontale Asymptote von Gf ist, und geben Sie die Gleichung der vertikalen Asymptoten von Gf an. Bestimmen Sie die Koordinaten des Schnittpunktes von Gf mit der y-Achse. Abbildung 1 zeigt den Graph der in IR definerten Funktion p:x > 0,5*(x+2)2 -0,5, die die Nullstelle x=-3 und x=-1 hat. Für x ∈ Df gilt c) Gemäß der Quotientenregel gilt für die Ableitung f' und p' die Beziehung Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x=-2 einzige Nullstelle von f' ist und dass Gf in ]-3;-2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunktes von Gf an. d) Berechnen Sie f(-5) und f(-1,5) und skizzieren Sie Gf unter Berücksichtigung der bisherigen Ergebnisse in Abbildung 1. |
Gegeben ist die Funktion a)Begründen Sie... |
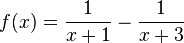 und Dafinitionsbereich Df = IR \ {-3;-1}. Der Graph von f wird mit Gf bezeichnet.
und Dafinitionsbereich Df = IR \ {-3;-1}. Der Graph von f wird mit Gf bezeichnet.
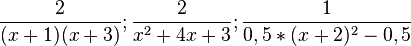
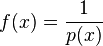 .
.
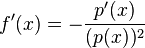 für x ∈ Df
für x ∈ Df
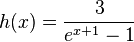 mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.


