Abi 2013 Analysis I Teil B
Aus RMG-Wiki
< Abitur Mathematik
Version vom 15. April 2018, 09:27 Uhr von Karina Hetterich (Diskussion | Beiträge)
|
|
Gegeben ist die in IR definierte Funktion a) Weisen Sie rechnerisch nach, dass Gf punktsymmetrisch bezüglich des Koordinatenursprungs ist, und machen Sie anhand des Funktionsterms
von f plausibel, dass b)Bestimmen Sie rechnerisch Lage und Art der Extrempunkte von Gf.
|
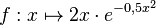 . Abbildung 2 zeigt den Graphen Gf von f.
. Abbildung 2 zeigt den Graphen Gf von f.
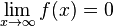 gilt.
gilt.

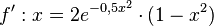 y-Koordinate des Hochpunkts: Fehler beim Parsen(Lexikalischer Fehler): \frac {2}{√e} <\math> :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] }} c) Berechnen Sie die mittlere Änderungsrate m<sub>S</sub> von f im Intervall [0,5; 0,5] sowie die lokale Änderungsrate m<sub>T</sub> von f an der Stelle x = 0 . Berechnen Sie, um wie viel Prozent m<sub>S</sub> von m<sub>T</sub> abweicht. :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] }} </td></tr></table></center> </div>
y-Koordinate des Hochpunkts: Fehler beim Parsen(Lexikalischer Fehler): \frac {2}{√e} <\math> :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1b_Lös.jpg|700px]] }} c) Berechnen Sie die mittlere Änderungsrate m<sub>S</sub> von f im Intervall [0,5; 0,5] sowie die lokale Änderungsrate m<sub>T</sub> von f an der Stelle x = 0 . Berechnen Sie, um wie viel Prozent m<sub>S</sub> von m<sub>T</sub> abweicht. :{{Lösung versteckt|1= [[Bild:ABI2017_AI_TeilB_1c_Lös.jpg|700px]] }} </td></tr></table></center> </div>

