2003 II
|
|
|
|
|
|
- Aufgabe 1
Gegeben ist die Schar der Funktionen  mit der maximalen Definitionsmenge Dk und k
mit der maximalen Definitionsmenge Dk und k  IR. Gk bezeichnet den Graphen von fk.
IR. Gk bezeichnet den Graphen von fk.
a) Bestimmen Sie für k < 0 und k > 0 jeweils die Definitionsmenge Dk. Untersuchen Sie für k 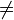 0 das Verhalten von fk für
0 das Verhalten von fk für 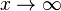 und
und 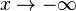 . Geben Sie die Gleichungen aller Asymptoten an.
. Geben Sie die Gleichungen aller Asymptoten an.
b) Zeigen Sie, dass gilt: 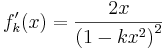 .
.
Begründen Sie, dass alle Graphen Gk einen gemeinsamen Tiefpunkt besitzen.
c) Skizzieren Sie G-1 und G1 in ein gemeinsames Koordinatensystem. Zeichnen Sie auch alle vorhandenen Asymptoten ein.
[[Bild:]]
d) Beschreiben Sie für den Fall k < 0, wie sich die Lage der waagerechten Asymptote von Gk für 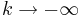 und
und 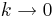 jeweils verändert.
jeweils verändert.
[[Bild:]]
e) Bestimmen Sie k zunächst so, dass Gk durch den Punkt P (1|2) verläuft.
Zeigen Sie dann, dass durch jeden beliebigen Punkt, der nicht auf einer der Koordinatenachsen liegt, genau ein Graph Gk verläuft.
[[Bild:]]
</td></tr></table></center>
</div>
Das nebenstehende Diagramm zeigt, wie die Geschwindigkeit eines Fahrzeugs von der Zeit abhängt; der zugehörige Funktionsterm für 0 Dabei bezeichnet v die Maßzahl der in Metern pro Sekunde gemessenen Geschwindigkeit, t die Maßzahl der in Sekunden gemessenen Zeit. Der Inhalt der Fläche zwischen dem Graphen, der t-Achse und der Geraden t = t0 entspricht dem während der ersten t0 Sekunden zurückgelegten Weg (in Metern).
[[Bild:]] 8 BE
[[Bild:]] 5 BE
|
 t
t 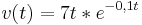 .
.

