2004 VI
Aus RMG-Wiki
< LK Mathematik | Abitur
Version vom 1. April 2010, 22:15 Uhr von Neutert Jan-Peter (Diskussion | Beiträge)
|
|
|
In einem kartesischen Koordinatensystem des R3 sind die Punkte
|
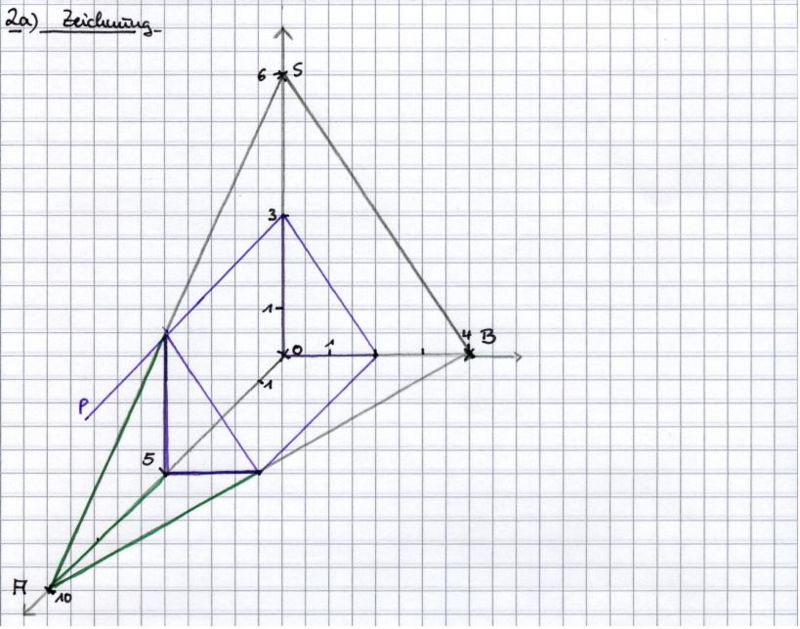
Die Punkte A, B, O und S bilden die Ecken der Pyramide ABOS.
(Hinweis: Zerlegen Sie einen der beiden Teilkörper in ein dreiseitiges Prisma und eine dreiseitige Pyramide.) |
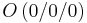 ,
, 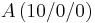 ,
, 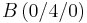 ,
, 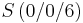 sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t
sowie die Ebenenschar Et: 3x2 + tx3 - 3t = 0 mit t  R gegeben. Die Punkte A, B und S legen die Ebene F fest.
R gegeben. Die Punkte A, B und S legen die Ebene F fest.


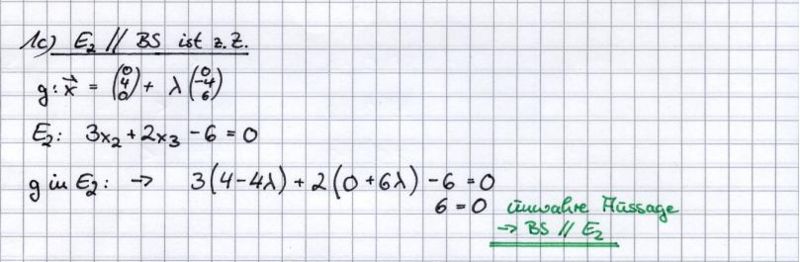



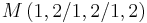 der Mittelpunkt der Inkugel K der Pyramide ABOS ist.
der Mittelpunkt der Inkugel K der Pyramide ABOS ist. 

