- Aufgabe 2
Die Ebene Et schneidet die x1-Achse im Punkt At, die x2-Achse im Punkt Bt und die x3-Achse im Punkt Ct. Diese Punkte und der Ursprung O sind für t ≠ 0 die Ecken einer Pyramide IIt.
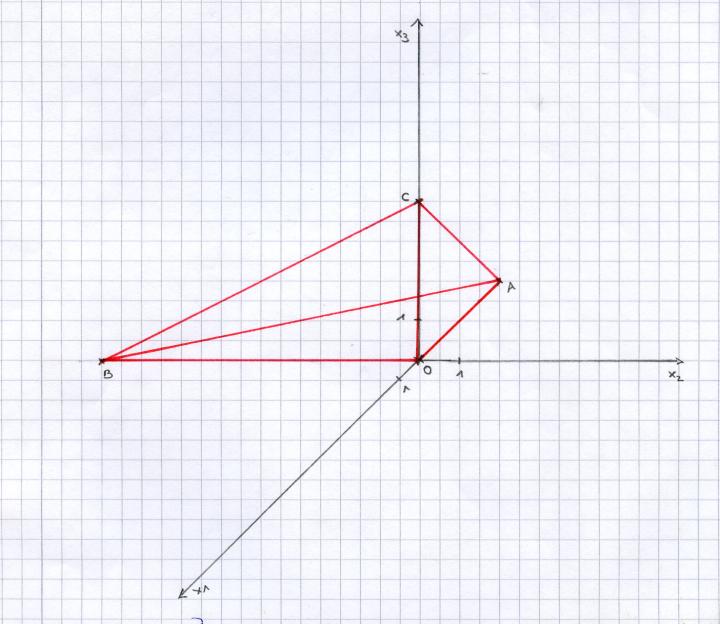
a) Berechnen Sie die Koordinaten der Punkte At, Bt und Ct und zeichnen Sie in einem Koordinatensystem für t = -8 die Pyramide II-8 ein.
[Teilergebnis: At (0,5t|0|0); Bt (0|t|0); Ct (0|0|-0,5t)]
- [Lösung anzeigen][Lösung ausblenden]

- Bemerkung
Andere Lösung bei der 2 a):
Man hätte die Achsengeraden aufstellen können, mit dem Ursprung als Aufpunkt und dem jeweiligen Richtungsvektor und dann den jeweiligen allg. Geradenpunkt in die Ebene einsetzen können.
b) Zeigen Sie, dass die Pyramide IIt den Oberflächeninhalt t2 besitzt, und ermitteln Sie das Volumen Vt von IIt in Abhängigkeit von t.
- [Lösung anzeigen][Lösung ausblenden]
c) Die Ebene F : 2x2 = t liegt parallel zu einer Seitenfläche und zerlegt IIt in zwei Teilkörper. Berechnen Sie das Verhältnis der Volumina.
- [Lösung anzeigen][Lösung ausblenden]
- Hinweis
-
Es gibt eine weitere Lösung, die den Strahlensatz verwendet (Verhältnis der beiden Höhen und der anderen Kanten ist 1:2)


d) Zeigen Sie, dass die Kugel K mit dem Mittelpunkt Nt (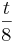 | |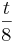 | |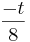 ) und dem Radius ρt = ) und dem Radius ρt = 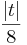 die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt. die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt.
- [Lösung anzeigen][Lösung ausblenden]
e) Die Ecken der Pyramide IIt liegen auf einer Kugel (Umkugel) mit dem Mittelpunkt M (m1|m2|m3) und dem Radius r.
Begründen Sie ohne weitere Rechnung, dass gilt: m2 = 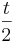 . .
Geben Sie m1 sowie m3 an und berechnen Sie r.
- [Lösung anzeigen][Lösung ausblenden]
| 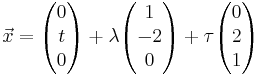 mit λ, τ є IR und t є IR gegeben.
mit λ, τ є IR und t є IR gegeben. 









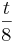 |
|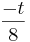 ) und dem Radius ρt =
) und dem Radius ρt = 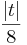 die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt.
die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt.




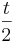 .
.


