- Aufgabe 2
Die Ebene E ist Tangentialebene an zwei Kukeln K1 und K2 mit dem Radius 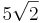 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen. , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
a) Bestimmen Sie die Koordinaten von M1 und M2 . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M1 bezeichnet.)
[Teilergebnis: (2/5/-6)]
6 BE
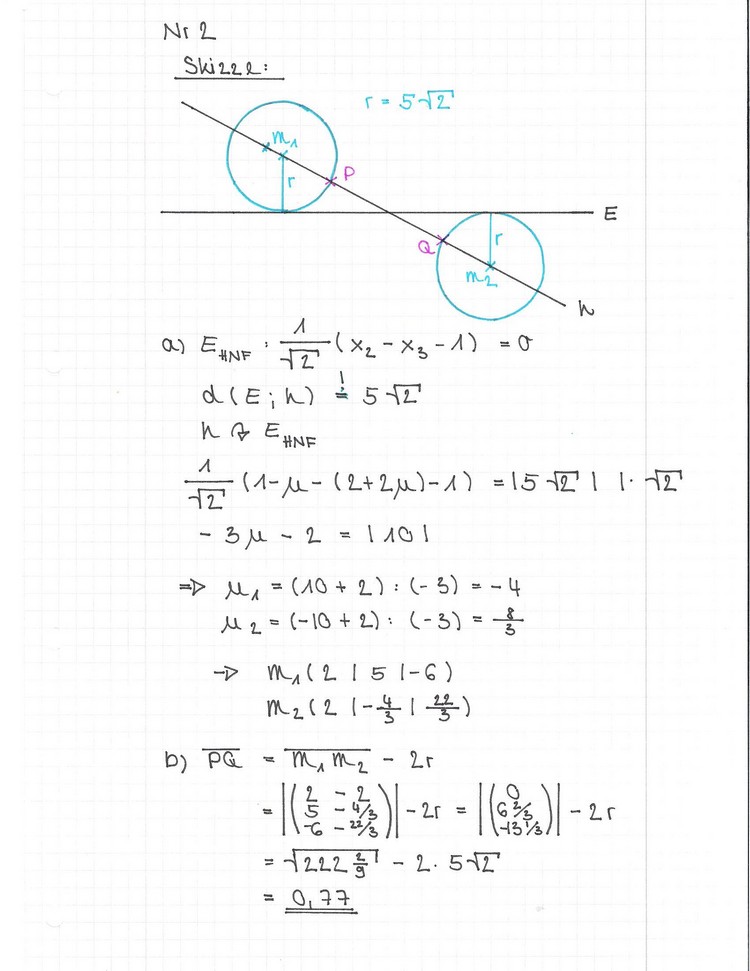
b) Die Kugelpunkte P  K1 und Q K1 und Q  K2 sind diejenigen Punkte, die minimale Distanz voneinander haben. Berechnen Sie die Entfernung [PQ] auf zwei Dezimalen gerundet. K2 sind diejenigen Punkte, die minimale Distanz voneinander haben. Berechnen Sie die Entfernung [PQ] auf zwei Dezimalen gerundet.
3 BE
- [Lösung anzeigen][Lösung ausblenden]
. 
c) Spiegelt man die Ebene E am Punkt M1, so erhält man die Ebene*. Geben Sie eine Gleichung von E* in Normalenform an.
4 BE
- [Lösung anzeigen][Lösung ausblenden]
.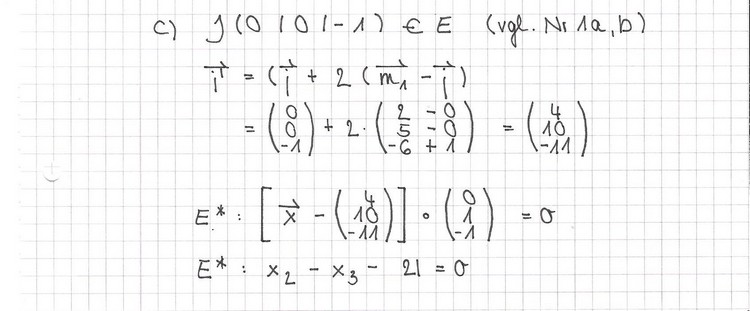
d) Zeigen Sie, dass die Punkte A (-1/0/-2) und C (-1/1/-1) auf der Kugel K1 um M1 liegen und bestimmen Sie die Koordinaten von B so, dass die Strecke [AB] ein Durchmesser von K1 ist.
[Teilergebnis: B (5/10/-10)]
4 BE
- [Lösung anzeigen][Lösung ausblenden]
. 
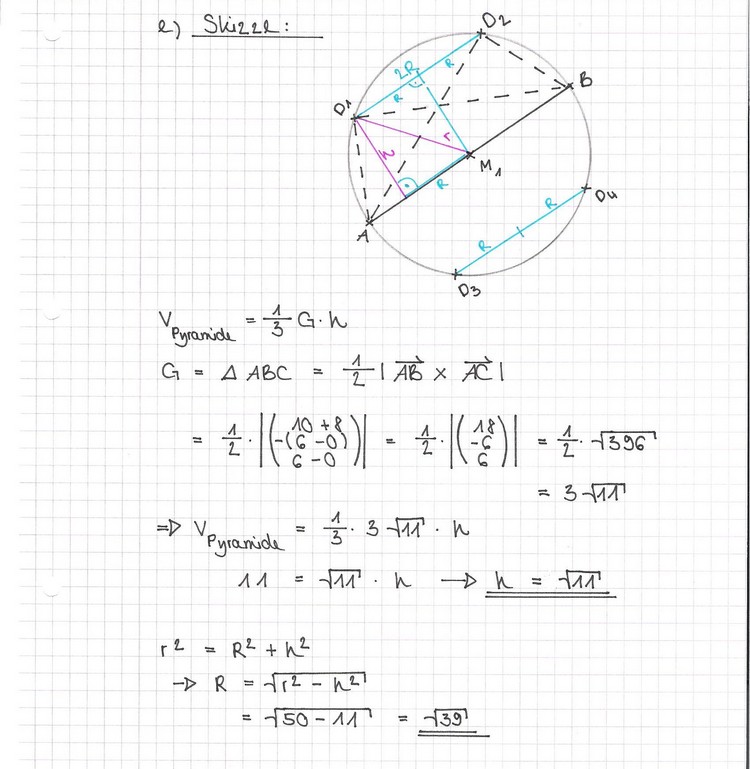
e) Das Dreieck ABC ist die Grundfläche einer Pyramide ABCD, deren Spitze D ebenfalls auf der Kugel K1 liegt. Alle Punkte D, für die die Pyramiden ABCD das Volumen 11 haben, bilden zwei Kreise auf der Kugelfläche (Nachweis nicht erforderlich).
Berechnen Sie zuerst die Höhe h dieser Pyramiden und anschließend mit Hilfe einer geeigneten Skizze den Radius R der beiden oben definierten Kreise.
[Zur Kontrolle: h = 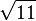 ] ]
6 BE
- [Lösung anzeigen][Lösung ausblenden]
. 
|