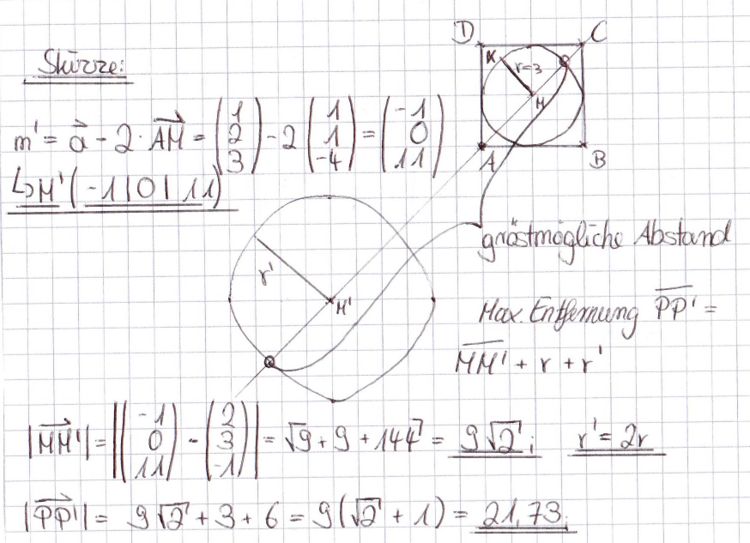2008 V
|
|
Aufgabe 1Gegeben sind in einem kartesischen Koordinatensystem des a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. (5 BE) Zur Kontrolle: E: 2x1+2x2+x3-9=0 b) Weisen Sie nach, dass sich die Punkte A, B und D durch einen vierten Punkt C zu einem Quadrat ABCD ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt M dieses Quadrats. (4 BE) Teilergebnis: M(2|3|-1) c) Für welchen Wert von t ist die Entfernung von St zu M minimal? (5 BE) Aufgabe 22) Das Quadrat ABCD als Begrenzungsfläche und die Strecke [DSt] als Seitenkante bestimmen ein Parallelflach. a) Berechnen Sie alle Werte von t, für die das Parallelflach den Rauminhalt V=144 hat. (6 BE) b) Bestimmen Sie t so, dass das Parallelflach ein Quader ist. (3 BE) Nun sei t=1. Die durch die Punkte A, D und S1 festgelegte Seitenfläche des Parallelflachs liegt in der Ebene F:2x1-x3+1=0. c) Im Punkt T(1|5|3) dieser Seitenfläche wird ein Lot errichtet. Berechnen Sie die Koordinaten des Punktes U, in dem das Lot die Ebene E schneidet, und zeigen Sie, dass U nicht im Innern des Quadrats ABCD liegt.(7 BE) d) Ermitteln Sie den Schnittwinkel der Ebenen E und F. (3 BE) Aufgabe 3K sei die Kugel, die den Punkt M aus Teilaufgabe 1b als Mittelpunkt und den Radius r=3 hat. Sie wird durch eine zentrische Streckung mit A als Zentrum und dem Streckungsfaktor -2 auf die Kugel K' abgebildet. Ermitteln Sie die Koordinaten des Mittelpunkts M' von K', sowie den maximalen Abstand, den zwei Punkte P und P' haben können, wenn P auf K und P' auf K' liegt. (7 BE)
|
 3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit
3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit 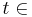

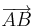
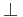
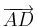 und
und 

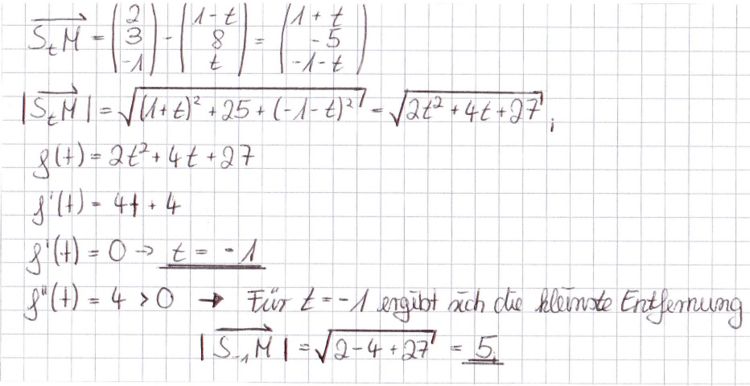
 Höhe
Höhe
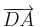 ,
,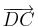 ,
,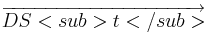 )
)