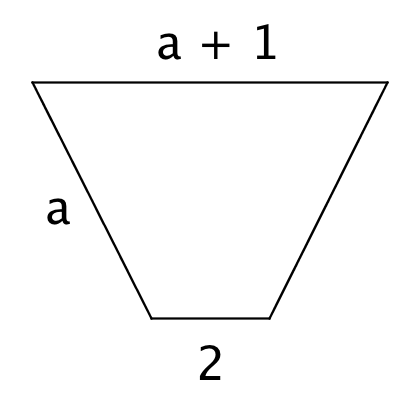
weiterführende Aufgaben

1. Berechne a so, dass der Umfang des Grundstücks größer als 100m ist!

a) b) c)

2. Werden alle Seiten eines Quadrates um jeweils 4 cm verlängert, so nimmt der Flächeninhalt um weniger als 40cm² zu. Berechne wie lang die Seiten des Quadrates sein können!

3. Begründe rechnerisch, dass die Punkte A (-1|1); B (5|1) & C (0|3) ein Dreieck bilden und berechne dessen Flächeninhalt!

4. Die Gerade h entsteht aus der Geraden g mit der Geradengleichung y = 2x - 5 durch Drehung um 90° im Punkt P (4|3). Gib die Geradengleichung der Geraden h an und überlege welche Gesetzmäßigkeit sich daraus folgern lässt!
Datei:Beispiel.jpg

5. Gegeben ist die Gerade g mit der Geradengleichung y = 2x - 1.
a) Berechne die Schnittpunkte mit den Koordinatenachsen!
b) Spiegle die Gerade g an der Winkelhalbierenden des 1. & 3. Quadranten und gib die Gleichung der neuen Geraden h an!
c) Welche Aussage kann man allgemein über einen Punkt machen, der an dieser Winkelhalbierenden gespiegelt wird?
d) Erschließe daraus allgemein die Gleichung einer Geraden, die durch Spiegelung der Geraden y = mx + t an der Winkelhalbierenden des 1. & 3. Quadranten entsteht!

6. Ein gleichschenkliges Dreieck mit der Basis b = x cm und der Schenkellänge s = y cm hat den Umfang 30 cm.
a) Den Zusammenhang zwischen Umfang, Basis- und Schenkellänge kann man durch eine lineare Funktion beschreiben. Wie lautet sie?
b) Zeichne den Graphen dieser Funktion!

7. Mario und Christian wohnen in einer Entfernung von 8 km voneinander und gehen sich gleichzeitig entgegen. Mario geht mit einer Geschwindigkeit von 5 km/h, Christian mit 4 km/h.
a) Wie lautet der Zusammenhang zwischen verstrichener Zeit und gegenseitiger Entfernung?
c) Wann treffen sich die beiden?

8. Ein Flugzeug befindet sich nach dem Start in einer Höhe von etwa 1000 m Höhe im Steigflug. Der Winkel zur Horizontalen beträgt ungefähr 10°.
a) Bestimme mit einem <zerlegungsparallelogramm die Geschwindigkeit in horizontaler Richtung und in Steigrichtung!
b) Wie lautet der Zusammenhang zwischen Flughöhe und Zeit?
c) Berechne nach wie vielen Minuten das Flugzeug seine Reisehöhe von 12000 m erreicht hat!
d) Welchen Weg hat das Flugzeug dann in horizontaler Richtung zurückgelegt?

9. Dreiecksungleichungen...
a) In einem Dreieck ist die erste Seite 10 cm, die zweite 15 cm lang. Überlege wie lang die dritte Seite mindestens bzw. höchstens ist!
b) Welche Ungleichungen werden wohl allgemein für die Seiten a, b, c eines Dreiecks gelten?
c) Wie lang kann eine Dreiecksseite maximal sein, wenn dessen Umfang 10 cm beträgt?

10. Der Betrag einer Zahl kann man mit deren Abstand auf dem Zahlenstrahl von der Null beschreiben. Veranschauliche die Lösungen der Ungleichungen auf einem Zahlenstrahl!
a) |x| > 3
b) |x - 2| < 1
c) |x| 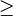$\ge$ 4