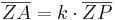Zentrische Streckung

Die Zentrische Streckung

Bei der bisher behandelten Abbildungen, wie Achsenspiegelung, Drehung, Verschiebung, die unter dem Namen Kongruenzabbildungen zusammengefasst werden, blieb die Größe unverändert. Eine Zentrische Streckung ist eine Abbildung, bei der Figuren vergrößert oder verkleinert werden können. Dies habt ihr bereits, ohne es zu wissen bei der Berechnug von Maßstäben genutzt.

Merke: Bei einer Zentrischen Streckung mit dem Streckzentrum Z und dem Streckfaktor k (k > 0) gilt für den Bildpunkt A zu einem Punkt P (P $\neq$ Z): A liegt auf der von Z ausgehenden Halbgeraden durch P ${\overline{ZA} = k \cdot \overline{ZP}\,}$

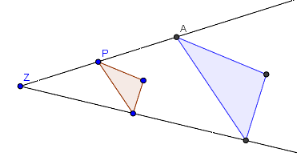
Die nachfolgende Abbildung zeigt die Zentrische Streckung des Fünfeckes ABCDE mit dem Streckzentrum Z und dem Streckfaktor k = 1,5. Mit Hilfe der Maus kannst du die blauen Punkte und die rote Fünfecksfläche verschieben. Dabei kannst du beobachten, wie sich die Beiden Fünfecksflächen verändern oder wie sich Punkt und Bildpunkt bzw. Strecke und Bildstrecke zueinander verhalten. Probier es aus!

Eigenschaften der Zentrischen Streckung:

1. Die Zentrische Streckung ist eine geradentreue Abbildung. Jede Gerade, die nicht durch das Streckzentrum verläuft wird auf eine zu ihr parallele Bildgerade abgebildet. z.B. [AB] || [A'B']
2. Die Zentrische Streckung ist verhältnistreu. Jede Urstrecke wird auf eine parallele Bildstrecke der k - fachen Länge abgebildet. z.B. $\overline{E'D'} = 1,5 \cdot \overline{ED}$
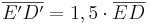
3. Die Zentrische Streckung ist eine winkeltreue Abbildung. Jeder Winkel wird auf einen gleich großen Winkel abgebildet.
4. Die Bildfigur hat den k² - fachen Flächeninhalt der Originalfigur.
   z.B.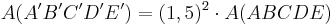 $A(A'B'C'D'E') = (1,5)^2 \cdot A(ABCDE)$)

Arbeitsauftrag:
Übertrage die Merksätze inkl. Erklärungsskizze unter der Überschrift "Die Zentrische Streckung" in dein Heft.

So sollte dein Hefteintrag aussehen

zum Inhaltsverzeichnis