Abzählmethode
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras
Version vom 1. Dezember 2008, 08:41 Uhr von Zehnder Moritz (Diskussion | Beiträge)
Der Satz des Pythagoras
|
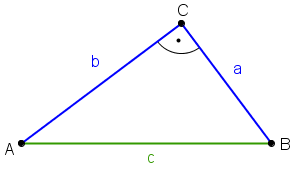
In rechtwinkligen Dreiecken mit den Katheten a und b und der Hypotenuse c gilt der Satz des Pythagoras:
|
Arbeitsauftrag:
- Zeichne das rechtwinklige Dreieck
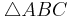 ab
ab
- Notiere dir den Satz des Pythagoras:
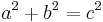
Die Abzählmethode
Es gibt neben dem Zerlegungsbeweis noch einen anderen Beweis zum Satz des Pythagoras.
Dieser funktioniert jedoch nur in rechtwinkligen Dreiecken mit ganzzahligen Seitenlängen!
Ganze Zahlen a, b und c, die die Gleichung 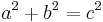 erfüllen, nennt man ein pythagoräisches Zahlentipel
erfüllen, nennt man ein pythagoräisches Zahlentipel
Man braucht also ein pythagoräisches Zahlentripel für die Abzählmethode.
Einige pythagoräische Zahlentripel sind:
| Kathetea | 3 | 6 | 5 | 7 |
| Katheteb | 4 | 8 | 12 | 24 |
| Hypotenuse | 5 | 10 | 13 | 25 |
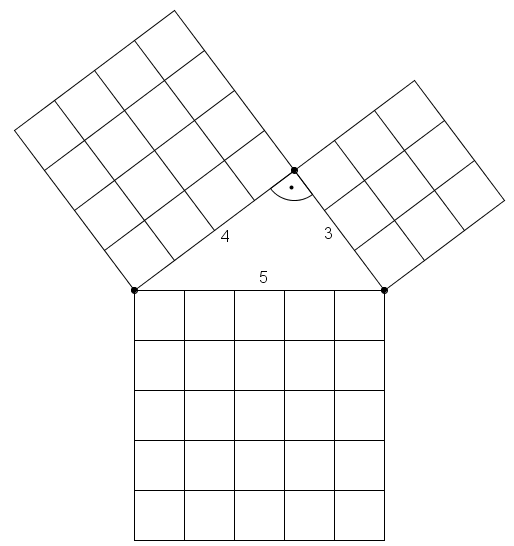
In der folgenden Zeichnung siehst du ein rechtwinkliges Dreieck mit einem pythagoräischen Zahlentripel als Seitenlängen:
Arbeitsauftrag:
- Zähle die einzelnen kleinen Quadrate ab, die in den Quadraten über den Katheten eingezeichnet sind
- Versuche mit den kleinen Quadraten das Quadrat über der Hypotenuse zu füllen
- Was fällt dir auf?
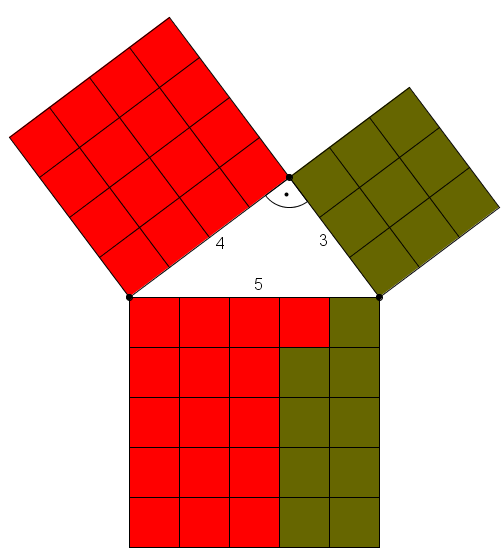
- Man kann die kleinen Quadrate von den Quadraten über den Katheten im Quadrat über der Hypotenuse verteilen
- Man sieht also dass sich die Quadrate über den Katheten auf das Quadrat über der Hypotenuse verteilen lassen
- d.h.
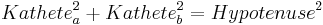
- Du hast damit den Satz des Pythagoras bewiesen!
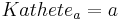 ,
, 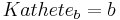 und
und 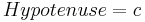 :
: