Abi 2015 Analysis I Teil B: Unterschied zwischen den Versionen
| Zeile 74: | Zeile 74: | ||
a) | a) | ||
| + | Begründen Sie anhand des Funktionsterms, dass <math>\lim_{x\to\infty}h(x)= 0</math> gilt.Zeigen Sie rechnerisch für hxD,dass für die Ableitung hvon h gilt:h x0.Gegeben ist ferner die in hD definierte Integralfunktion x00H : xh t dt. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2015_AI_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2015_AI_TeilB_2a_Lös.jpg|700px]] | ||
Version vom 26. Juli 2017, 08:34 Uhr
|
|
Gegeben ist die Funktion f mit
b) Begründen Sie, dass die x-Achse horizontale Asymptote von Gf ist, und geben Sie die Gleichungen der vertikalen Asymptoten von Gf an. Be-
stimmen Sie die Koordinaten des Schnittpunkts von Gf mit der y-Achse. Abbildung 1 zeigt den Graphen der in IR definierten Funktion Für x ∈ Df gilt c) Gemäß der Quotientenregel gilt für die Ableitungen f' und p' die Beziehung: Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von f'(x) und p'(x), dass x = -2 einzige Nullstelle von f' ist und dass Gf in ]-3; -2[ streng monoton steigend sowie in ]-2;-1[ streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von Gf an. d) Berechnen Sie f(-5) und f(-1,5) und skizzieren sie Gf unter Berücksichtigung der Ergebnisse in Abbildung 1. |
Gegeben ist die Funktion a)
Begründen Sie anhand des Funktionsterms, dass b) c)
|
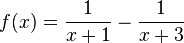 und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
und Definitionsbereich Df = IR\{-3; -1}. Der Graph vonf wird mit Gf bezeichnet.
a) Zeigen Sie, dass f(x) zu jedem der drei folgenden Terme äquivalent ist:
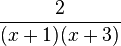 ;
;
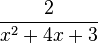 ;
;
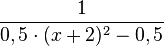

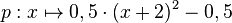 , die die Nullstellen x = -3 und x = -1 hat.
, die die Nullstellen x = -3 und x = -1 hat.
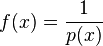 .
.

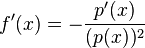 für x ∈ Df.
für x ∈ Df.


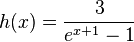 mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
mit Definitionsbereich Dh = ]-1;+∞[. Abbildung 2 zeigt den Graph Gh von h.
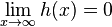 gilt.Zeigen Sie rechnerisch für hxD,dass für die Ableitung hvon h gilt:h x0.Gegeben ist ferner die in hD definierte Integralfunktion x00H : xh t dt.
gilt.Zeigen Sie rechnerisch für hxD,dass für die Ableitung hvon h gilt:h x0.Gegeben ist ferner die in hD definierte Integralfunktion x00H : xh t dt.

