Abi 2016 Analysis I Teil B: Unterschied zwischen den Versionen
| Zeile 40: | Zeile 40: | ||
c) | c) | ||
| − | Zeigen Sie, dass für die zweite Ableitung f'' von f die Beziehung <math>f''(x)=\frac{1}{4}*f(x)</math> für | + | Zeigen Sie, dass für die zweite Ableitung f'' von f die Beziehung <math>f''(x)=\frac{1}{4}*f(x)</math> für x∈IR gilt. Weisen Sie nach, dass G<sub>f</sub> linksgekrümmt ist. (Zur Kontrolle <math> f'(x)= \frac{1}{2}\cdot (e^{\frac{1}{2}x}- e^{-\frac{1}{2}x}) </math> ) |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_AI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2016_AI_TeilB_1c_Lös.jpg|700px]] | ||
| Zeile 81: | Zeile 81: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | a) | + | a)Die Enden eines Seils werden |
| + | an zwei vertikalen Masten, die | ||
| + | 8,00 m voneinander entfernt | ||
| + | sind, in gleicher Höhe über | ||
| + | dem Erdboden befestigt. Der | ||
| + | Graph G<sub>f</sub> aus Aufgabe 1 be- | ||
| + | schreibt im Bereich <math> | ||
| + | -4 \le x \ge 4 </math> | ||
| + | modellhaft den Verlauf des | ||
| + | Seils, wobei die Fußpunkte | ||
| + | F<sub>1</sub> | ||
| + | und | ||
| + | 2 | ||
| + | F | ||
| + | der Masten durch die | ||
| + | Punkte | ||
| + | | ||
| + | 4|0 | ||
| + | | ||
| + | bzw. | ||
| + | | ||
| + | 4|0 | ||
| + | dargestellt werden (vgl. Abbildung) | ||
| + | . Eine Längeneinheit im Koordinaten- | ||
| + | system entspricht einem | ||
| + | Meter in der Realität. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_AI_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2016_AI_TeilB_2a_Lös.jpg|700px]] | ||
Version vom 26. Juli 2017, 08:23 Uhr
|
|
Gegeben ist die in IR definierte Funktion a) Bestimmen Sie die Koordinaten des Schnittpunktes von Gf mit der y-Achse und begünden Sie, dass Gf oberhalb der x-Achse verläuft. b) Ermitteln Sie das Symmetrieverhalten von Gf sowie das Verhalten von f für x→-∞ x→+∞. c)
Zeigen Sie, dass für die zweite Ableitung f von f die Beziehung d) e) f) g) h) |
a)Die Enden eines Seils werden
an zwei vertikalen Masten, die
8,00 m voneinander entfernt
sind, in gleicher Höhe über
dem Erdboden befestigt. Der
Graph Gf aus Aufgabe 1 be-
schreibt im Bereich der Masten durch die Punkte 4|0 bzw. 4|0 dargestellt werden (vgl. Abbildung) . Eine Längeneinheit im Koordinaten- system entspricht einem Meter in der Realität. b) c) d) |
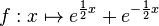 . Der Graph von f wird
mit Gf bezeichnet.
. Der Graph von f wird
mit Gf bezeichnet.
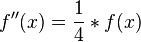 für x∈IR gilt. Weisen Sie nach, dass Gf linksgekrümmt ist. (Zur Kontrolle
für x∈IR gilt. Weisen Sie nach, dass Gf linksgekrümmt ist. (Zur Kontrolle 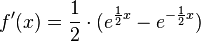 )
)
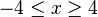 modellhaft den Verlauf des
Seils, wobei die Fußpunkte
F1
und
2
F
modellhaft den Verlauf des
Seils, wobei die Fußpunkte
F1
und
2
F

