Abi 2016 Analysis I Teil A: Unterschied zwischen den Versionen
| Zeile 111: | Zeile 111: | ||
Die Abbildung zeigt den Graphen der in IR definierten Funktion f. | Die Abbildung zeigt den Graphen der in IR definierten Funktion f. | ||
[[Bild:ABI2016_AI_TeilA_5.jpg|center|350px]] | [[Bild:ABI2016_AI_TeilA_5.jpg|center|350px]] | ||
| − | a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für <math> \int_{5}^{3} f (x)\,dx</math>. | + | a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für <math> \int_{5}^{3} f (x)\,dx </math>. |
Die Funktion F ist die in IR definierte Stammfunktion von f mit F(3)=0. | Die Funktion F ist die in IR definierte Stammfunktion von f mit F(3)=0. | ||
b) Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von F an der Stelle x=2 an. | b) Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von F an der Stelle x=2 an. | ||
| − | c) Zeigen Sie, dass | + | c) Zeigen Sie, dass F(b)= <math> \int_{b}^{3} f (x)\,dx <\math> mit b ∈ IR gilt. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 26. Juli 2017, 08:20 Uhr
|
|
1
Gegeben ist die Funktion
a) Bestimmen Sie D. b)
Bestimmen Sie den Wert x∈D mit
|
Zeigen Sie, dass der Graph der in IR definierten Funktion an |
Skizzieren Sie im Bereich |
Gegeben ist eine in IR definierte ganzrationale Funktion f dritten Grades, deren Graph f an der Stelle x=1 einen Hochpunkt und an der Stelle x=4 einen Tiefpunkt besitzt. a) Begründen Sie, dass der Graph der Ableitungsfunktion f' von f eine Parabel ist, welche die x-Achse in den Punkten (1|0) und (4|0) schneidet und nach oben geöffnet ist. b) Begründen Sie, dass 2,5 die x-Koordinate des Wendepunkts vom Graphen f ist. |
Die Abbildung zeigt den Graphen der in IR definierten Funktion f. a) Bestimmen Sie mithilfe der Abbildung einen Näherungswert für Die Funktion F ist die in IR definierte Stammfunktion von f mit F(3)=0. b) Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von F an der Stelle x=2 an. c) Zeigen Sie, dass F(b)= Fehler beim Parsen(Unbekannte Funktion „\math“): \int_{b}^{3} f (x)\,dx <\math> mit b ∈ IR gilt. :{{Lösung versteckt|1= [[Bild:ABI2016_AI_TeilA_5abc_Lös.jpg|700px]] }} </td></tr></table></center> </div> |
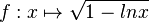 mit maximaler Definitionsmenge D.
mit maximaler Definitionsmenge D.
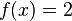
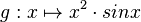 punktsymmetrisch bezüglich des Koor
dinatenursprungs ist, und geben Sie
den Wert des Integrals
punktsymmetrisch bezüglich des Koor
dinatenursprungs ist, und geben Sie
den Wert des Integrals
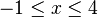 den Graphen einer in IR definierten Funktion f mit den folgenden Eigenschaften:
f ist nur an der Stelle x=3 nicht differenzierbar.
f(0)=2 und für die Ableitung f´ von f gilt: f´(0)=-1.
Der Graph von f ist im Bereich -1<x<3 linksgekrümmt.
den Graphen einer in IR definierten Funktion f mit den folgenden Eigenschaften:
f ist nur an der Stelle x=3 nicht differenzierbar.
f(0)=2 und für die Ableitung f´ von f gilt: f´(0)=-1.
Der Graph von f ist im Bereich -1<x<3 linksgekrümmt.
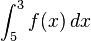 .
.

