Abi 2016 Analysis I Teil B: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 40: | Zeile 40: | ||
c) | c) | ||
| − | Zeigen Sie, dass für die zweite Ableitung f'' von f die Beziehung <math>f''(x)=\frac{1}{4}*f(x)</math> für | + | Zeigen Sie, dass für die zweite Ableitung f'' von f die Beziehung <math>f''(x)=\frac{1}{4}*f(x)</math> für x ∈ IR gilt. Weisen Sie nach, dass G<sub>f</sub> linksgekrümmt ist. |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2016_AI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2016_AI_TeilB_1c_Lös.jpg|700px]] | ||
Version vom 26. Juli 2017, 08:06 Uhr
|
|
Gegeben ist die in IR definierte Funktion a) Bestimmen Sie die Koordinaten des Schnittpunktes von Gf mit der y-Achse und begünden Sie, dass Gf oberhalb der x-Achse verläuft. b) Ermitteln Sie das Symmetrieverhalten von Gf sowie das Verhalten von f für x→-∞ x→+∞. c)
Zeigen Sie, dass für die zweite Ableitung f von f die Beziehung d) e) f) g) h) |
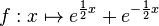. Der Graph von f wird
mit Gf bezeichnet.
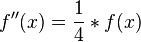für x ∈ IR gilt. Weisen Sie nach, dass Gf linksgekrümmt ist.
