Abi 2016 Analysis II Teil A: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | 1) Gegeben ist die Funktion <math>f(x)= \frac{ln(x)}{x^2}</math> mit maximalem Definitionsbereich D. <br> | + | 1) Gegeben ist die Funktion <math>f(x)= \frac{ln(x)}{x^2}</math> mit maximalem Definitionsbereich D. <br> <br> |
| − | + | a) Geben Sie D sowie die Nullstelle von f an und bestimmen Sie <math>\lim_{x\to 0}</math> f(x). <br> <br> | |
| − | + | b) Ermitteln Sie die x-Koordinate des Punkts, in dem der Graph von f eine | |
| − | + | ||
| − | + | ||
waagrechte Tangente hat. | waagrechte Tangente hat. | ||
Version vom 12. Juli 2017, 08:28 Uhr
|
|
1) Gegeben ist die Funktion
|
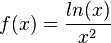mit maximalem Definitionsbereich D. 
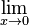f(x).
|
|
