Abituraufgaben zu bedingten Wahrscheinlichkeiten: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 181: | Zeile 181: | ||
b) Ermitteln Sie die Wahrscheinlichkeit dafür, dass ein nach der Kontrolle zufällig ausgewähltes Bauteil fehlerhaft ist, wenn es im Rahmen der Kontrolle als einwandfrei eingestuft wurde. | b) Ermitteln Sie die Wahrscheinlichkeit dafür, dass ein nach der Kontrolle zufällig ausgewähltes Bauteil fehlerhaft ist, wenn es im Rahmen der Kontrolle als einwandfrei eingestuft wurde. | ||
| − | |||
</popup> | </popup> | ||
| Zeile 187: | Zeile 186: | ||
====Aufgabe 11: Übungsklausur==== | ====Aufgabe 11: Übungsklausur==== | ||
| − | |||
ausführliche [[Abituraufgaben zu bedingten Wahrscheinlichkeiten/Lösung Übungsklausur|Lösung]] | ausführliche [[Abituraufgaben zu bedingten Wahrscheinlichkeiten/Lösung Übungsklausur|Lösung]] | ||
====Aufgabe 12: Übungsklausur - Nachschrift==== | ====Aufgabe 12: Übungsklausur - Nachschrift==== | ||
| − | |||
ausführliche [[Abituraufgaben zu bedingten Wahrscheinlichkeiten/Lösung Übungsklausur-Nachschrift|Lösung]] | ausführliche [[Abituraufgaben zu bedingten Wahrscheinlichkeiten/Lösung Übungsklausur-Nachschrift|Lösung]] | ||
Version vom 8. Februar 2015, 15:26 Uhr
alle Aufgaben als pdf-Datei
Originalaufgaben zum Download oder Ausdrucken
Aufgabe 1: Abitur 2014 - 1A
ausführliche Lösung
Aufgabe 2: Abitur 2014 - 1B
ausführliche Lösung
Aufgabe 3: Abitur 2013 - 1
ausführliche Lösung
Aufgabe 4: Abitur 2013 - 2
ausführliche Lösung
Aufgabe 5: Abitur 2012 - 1
ausführliche Lösung
Aufgabe 6: Abitur 2012 - 2
ausführliche Lösung
Aufgabe 7: Abitur 2011 - 1
ausführliche Lösung
Aufgabe 8: Abitur 2011 - 2
ausführliche Lösung
Aufgabe 9: Musterabitur 2011
ausführliche Lösung
Aufgabe 10: Aufgabe aus länderübergreifendem Aufgabenpool
ausführliche Lösung
Aufgabe 11: Übungsklausur
ausführliche Lösung
Aufgabe 12: Übungsklausur - Nachschrift
ausführliche Lösung
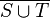 im Sachzusammenhang.
im Sachzusammenhang.
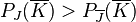 gilt.
Begründen Sie, dass es trotz der Gültigkeit dieser Ungleichung nicht sinnvoll ist, sich im Wahlkampf vo
rwiegend auf die Jungwähler zu konzentrieren.
gilt.
Begründen Sie, dass es trotz der Gültigkeit dieser Ungleichung nicht sinnvoll ist, sich im Wahlkampf vo
rwiegend auf die Jungwähler zu konzentrieren.
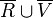 im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses.
im Sachzusammenhang und bestimmen Sie die Wahrscheinlichkeit dieses Ereignisses.