Funktionen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Teste dein Wissen) |
|||
| Zeile 77: | Zeile 77: | ||
{ | { | ||
| type="{}" } | | type="{}" } | ||
| − | <math>f(x)=\frac 1 x + \frac 3 | + | <math>f(x)=\frac 1 x + \frac 6 3 \qquad \lim_{x \to \infty}f(x)= </math> { 2 } |
| − | <math>f(x)=\frac 1 x + \frac 3 | + | <math>f(x)=\frac 1 x + \frac 6 3 \qquad \lim_{x \to -\infty}f(x)= </math> { 2 } |
| − | + | <br/> | |
| − | <math>f(x)=\frac { | + | <math>f(x)=\frac {6x^5+4x^2} {x^2+3x^4} \qquad \lim_{x \to \infty}f(x)= </math> { u } |
| − | <math>f(x)=\frac { | + | <math>f(x)=\frac {6x^5+4x^2} {x^2+3x^4} \qquad \lim_{x \to -\infty}f(x)= </math> { -u } |
| − | + | <br/> | |
| − | <math>f(x)=\frac {3x^2-x | + | <math>f(x)=\frac {3x^2-x+6x^5} {3x^5+x+1} \qquad \lim_{x \to \infty}f(x)= </math> { 2 } |
| − | <math>f(x)=\frac {3x^2-x | + | <math>f(x)=\frac {3x^2-x+6x^5} {3x^5+x+1} \qquad \lim_{x \to -\infty}f(x)= </math> { 2 } |
| − | + | <br/> | |
<math>f(x)=\frac 3 5 x^3 + \frac 3 5 x^2 \qquad \lim_{x \to \infty}f(x)= </math> { u } | <math>f(x)=\frac 3 5 x^3 + \frac 3 5 x^2 \qquad \lim_{x \to \infty}f(x)= </math> { u } | ||
<math>f(x)=\frac 3 5 x^3 + \frac 3 5 x^2 \qquad \lim_{x \to -\infty}f(x)= </math> { -u } | <math>f(x)=\frac 3 5 x^3 + \frac 3 5 x^2 \qquad \lim_{x \to -\infty}f(x)= </math> { -u } | ||
| − | + | <br/> | |
<math>f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to \infty}f(x)= </math> { Null } | <math>f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to \infty}f(x)= </math> { Null } | ||
<math>f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to -\infty}f(x)= </math> { u } | <math>f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to -\infty}f(x)= </math> { u } | ||

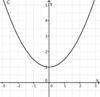
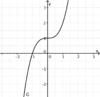
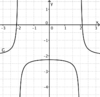
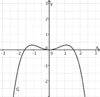
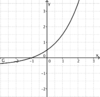
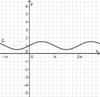
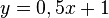
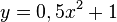
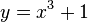
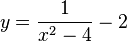
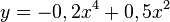
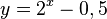
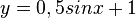
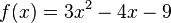 liegt.
(Nein, P liegt unterhalb von Gf)
(!Nein, P liegt oberhalb von Gf)
(!Ja, P liegt auf Gf)
liegt.
(Nein, P liegt unterhalb von Gf)
(!Nein, P liegt oberhalb von Gf)
(!Ja, P liegt auf Gf)
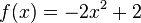 die richtige Aussage an:
die richtige Aussage an:
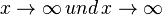 an.
an.  und "-u" für
und "-u" für 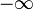 .
. 
