2010 IV: Unterschied zwischen den Versionen
| Zeile 195: | Zeile 195: | ||
<tr> | <tr> | ||
<td> p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | <td> p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | ||
| − | <td>A<sub>1</sub> {0,...,k}</td> | + | <td>A<sub>1</sub> = {0,...,k}</td> |
<td> <math> P_{\frac {1}{5}}^{25} (x \ge k+1) </math></td> | <td> <math> P_{\frac {1}{5}}^{25} (x \ge k+1) </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | <td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | ||
| − | <td>A<sub>2</sub> {k+1,...,25}</td> | + | <td>A<sub>2</sub> = {k+1,...,25}</td> |
<td><math> P_{\frac {1}{3}}^{25} (x \le k) </math></td> | <td><math> P_{\frac {1}{3}}^{25} (x \le k) </math></td> | ||
</tr> | </tr> | ||
| Zeile 228: | Zeile 228: | ||
<tr> | <tr> | ||
<td>p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | <td>p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | ||
| − | <td>A<sub>1</sub> {0,...,6}</td> | + | <td>A<sub>1</sub> = {0,...,6}</td> |
<td><math> P_{\frac {1}{5}}^{25} (x \ge 7) </math></td> | <td><math> P_{\frac {1}{5}}^{25} (x \ge 7) </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | <td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | ||
| − | <td>A<sub>2</sub> {7,...,25}</td> | + | <td>A<sub>2</sub> = {7,...,25}</td> |
<td> <math> P_{\frac {1}{3}}^{25} (x \le 6) </math></td> | <td> <math> P_{\frac {1}{3}}^{25} (x \le 6) </math></td> | ||
</tr> | </tr> | ||
| Zeile 265: | Zeile 265: | ||
<tr> | <tr> | ||
<td> p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | <td> p<sub>A</sub> = <math> \textstyle \frac {1}{5}</math></td> | ||
| − | <td>A<sub>1</sub> {0,...,4}</td> | + | <td>A<sub>1</sub> = {0,...,4}</td> |
<td> <math> P_{\frac {1}{5}}^{25} (x \ge 5) </math></td> | <td> <math> P_{\frac {1}{5}}^{25} (x \ge 5) </math></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | <td>p<sub>B</sub> = <math> \textstyle \frac {1}{3}</math></td> | ||
| − | <td>A<sub>2</sub> {5,...,25}</td> | + | <td>A<sub>2</sub> = {5,...,25}</td> |
<td><math> P_{\frac {1}{3}}^{25} (x \le 4) </math></td> | <td><math> P_{\frac {1}{3}}^{25} (x \le 4) </math></td> | ||
</tr> | </tr> | ||
Aktuelle Version vom 28. Februar 2011, 23:17 Uhr
|
|
Es gibt zwei Typen A und B von Jumbo-Verkaufspackungen, die jeweils
gut gemischt Tausende von Bausteinen enthalten; diese unterscheiden sich
nur in ihrer Farbe. Bei Typ A ist jeder fünfte, bei Typ B jeder dritte Baustein
gelb. a) Geben Sie die Entscheidungsregel an, bei der die beiden Wahrscheinlichkeiten, sich irrtümlich für einen falschen Typ zu entscheiden, möglichst nahe beieinander liegen. Wie groß sind in diesem Fall die beiden Irrtumswahrscheinlichkeiten? (5 BE) Für Typ A gilt: Jeder 5. Baustein ist gelb. Daraus folgt: pA =
k = 5: 0,61669 + 0,11195 = 0,72864 Man entscheidet sich bei höchstens 6 gelben Steinen für pA.
Die Fehlerwahrscheinlichkeiten lauten also:
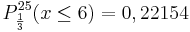 b) Wie muss die Entscheidungsregel aus Teilaufgabe 2a bei gleichbleibendem Stichprobenumfang geändert werden, wenn man die Wahrscheinlichkeit, sich irrtümlich für Typ A zu entscheiden, verringern will? Nennen Sie eine Konsequenz, die diese Änderung hinsichtlich einer Entscheidung für Typ B hat. (3 BE) Antwort: Wenn man die die Wahrscheinlichkeit, sich fälschlicherweise für Typ A zu entscheiden, verringern will, so muss der Annahmebereich A1 kleiner werden. Also k < 6.
So folgt z.B. für k = 4:
Antwort: Die Konsequenz davon ist, dass die Wahrscheinlichkeit sich fälschlicherweise für Typ B zu entscheiden steigt. |
Lars’ kleine Schwester spielt mit 3 roten, 4 blauen und 3 gelben würfelförmigen
Bausteinen, die sich nur in ihrer Farbe unterscheiden. a) Sie baut einen Turm, indem sie alle Steine aufeinandersetzt. Wie viele
verschiedene Farbmuster sind bei diesem Turm möglich, wenn weder
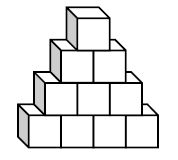
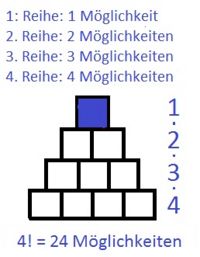
der oberste noch der unterste Stein rot sein sollen? (4 BE) Der Turm schaut wie folgt aus (liegend dargestellt): Antwort: Es gibt 1960 verschiedene Farbmuster. b) Nun baut sie aus den 10 Steinen eine „Treppe“ (siehe Abbildung). Wie viele verschiedene Farbmuster sind für die aus 10 Quadraten bestehende Stirnseite der „Treppe“ möglich, wenn in jeder waagrechten Reihe ein blauer Stein sitzen soll? (4 BE) Da in jeder waagrechten Reihe ein blauer Stein sitzen soll schauen die Verteilungsmöglichkeiten für blaue Steine wie folgt aus: Nun bleiben noch 6 Plätze für die gelben Steine übrig: Antwort: Es ergeben sich also 24  20 = 480 verschieden Farbmuster für die "Treppe", wenn in jeder waagrechten Reihe ein blauer Stein sitzt. 20 = 480 verschieden Farbmuster für die "Treppe", wenn in jeder waagrechten Reihe ein blauer Stein sitzt. |
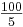 = 20 gelbe Steine.
= 20 gelbe Steine.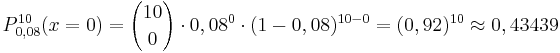
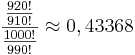
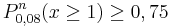
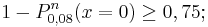
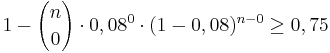 ;
;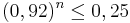 ;
;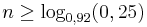 ;
;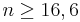 ;
;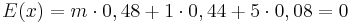 ;
;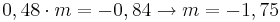 ;
;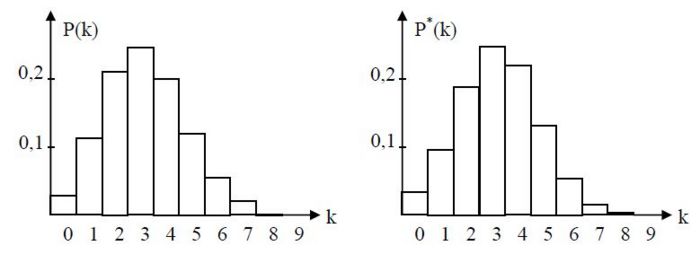
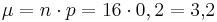
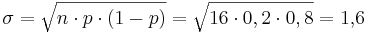
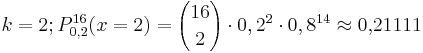
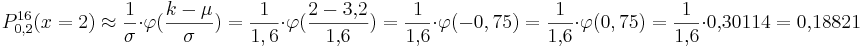
 stammen aus dem Tafelwerk.
stammen aus dem Tafelwerk. 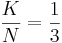 ;
;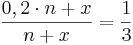 ;
;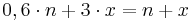 ;
;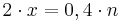 ;
;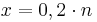 ;
;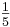 .
.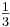 .
.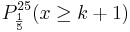
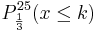
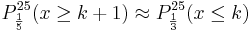
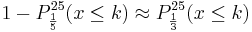
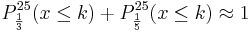
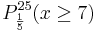
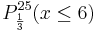
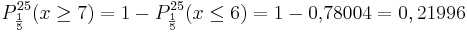
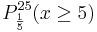
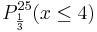

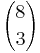 Möglichkeiten.
Möglichkeiten.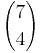 Möglichkeiten ergibt.
Möglichkeiten ergibt.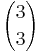
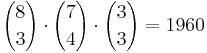 Möglichkeiten.
Möglichkeiten.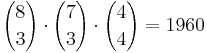
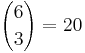 Möglichkeiten ergibt.
Möglichkeiten ergibt. 
