Quint-System: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
<math>\frac{H(A)}{H(B)} = \frac{2}{1} ; </math><br><br> | <math>\frac{H(A)}{H(B)} = \frac{2}{1} ; </math><br><br> | ||
| − | <math>\frac{H(A)}{H(B)} = 3 | + | <math>\frac{H(A)}{H(B)} = \frac {3} {2} </math> im Falle einer Quinte;<br><br> |
| − | <math>\frac{H(A)}{H(B)} = 4 | + | <math>\frac{H(A)}{H(B)} = \frac {4}{3} </math> im Falle einer Quarte;</math><br><br> |
Dies waren die Proportionen, die besonderen Wohlklang erzeugten. Nun versuchte Pythagoras mit Hilfe der Quinte die Oktave ins 6 gleichgroße Schritte zu zerlegen. Indem er zuerst 2 Quinten aufwärts und dann wieder eine Oktave abwärts ging erhielt er folgendes Verhältnis: | Dies waren die Proportionen, die besonderen Wohlklang erzeugten. Nun versuchte Pythagoras mit Hilfe der Quinte die Oktave ins 6 gleichgroße Schritte zu zerlegen. Indem er zuerst 2 Quinten aufwärts und dann wieder eine Oktave abwärts ging erhielt er folgendes Verhältnis: | ||
| Zeile 125: | Zeile 125: | ||
<br><br> [[Grieninger Sebastian/Facharbeit1/reine Stimmung|weiter zur reinen Stimmung]]<br><br> | <br><br> [[Grieninger Sebastian/Facharbeit1/reine Stimmung|weiter zur reinen Stimmung]]<br><br> | ||
| − | + | <br>[[Grieninger Sebastian/Facharbeit1|zur Übersicht]]<br><br> | |
---- | ---- | ||
<references /> | <references /> | ||
Version vom 22. Dezember 2010, 17:21 Uhr
Inhaltsverzeichnis |
Die pythagoreische Stimmung
Sie geht auf Pythagoras von Samos zurück. Die verschiedenen Intervalle wurden in der Antike von den Pythagoreern experimentell vom Monochord abgeleitet. Die abgeleiteteten Zahlenverhältnisse wurden durch die Proportionen der klingenden Seitenlängen hörbar gemacht. Pythagoras von Samos erkannte, der Schmiedlegende nach, als erster den Zusammenhang zwischen den Zahlenverhältnissen und den Tonabständen.
Sein System baut auf den beiden Intervallen Quinte Q und Oktave Ok auf, denn zu allen anderen Intervallen die es in diesem System gibt, existieren natürliche Zahlen (n,m) für die gilt: 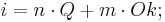
Aus dieser Gleichung wird deutlich das sich alle anderen Intervalle als Linearkombination der beiden darstellen lassn.
Die pythagoreische Stimmung, ist ein Quint-System, in der ausgehend von Quinte und Oktave alle Töne eingeteilt werden.
Für Interessierte: Brief des Guido von Arezzo (Beschreibung der pythagoreischen Stimmung)
Die Berechnung der Töne in der pythagoreischen Stimmung:
Allgemein lässt sich hier die Höhe des Tones mit folgender Formel wiedergeben:
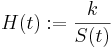
H(t) ist die Tonhöhe; S(t) die Saitenlänge (in einer beliebigen Längeneinheit); k ist eine feste Konstante.
Für zwei Töne, A und B, gilt, wenn sie eine Oktave auseinanderliegen:
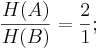
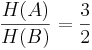 im Falle einer Quinte;
im Falle einer Quinte;
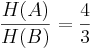 im Falle einer Quarte;</math>
im Falle einer Quarte;</math>
Dies waren die Proportionen, die besonderen Wohlklang erzeugten. Nun versuchte Pythagoras mit Hilfe der Quinte die Oktave ins 6 gleichgroße Schritte zu zerlegen. Indem er zuerst 2 Quinten aufwärts und dann wieder eine Oktave abwärts ging erhielt er folgendes Verhältnis:
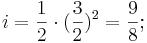 das Verhältnis der Sekunde.
das Verhältnis der Sekunde.
Mit A0 als Grundton und der Höhe H(A0) = 1 konstruierte er die anderen 6 Tonhöhen A1,A2,...A6;
Berechnung der Intervalle in der pythagoreischen Stimmung
Man kann alle Töne nach der auf der auf der vorgehenden Seite angegebenen Formel berechnen. Aus den verschiedenen Tonhöhen enthält man die verschiedenen Intervalle.
Die pythagoreische Stimmung setzt sich aus fünf großen und zwei kleinen Tonschritten zusammen.
Den großen Tonschritt haben wir bereits berechnet.
Er beträgt 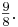
Alternativ kann man ihn berechnen, wenn man von einer Quinte eine Quarte abzieht:
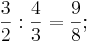
Der kleine Tonschritt, der Halbton ergibt sich, wenn man von der Quarte zwei Ganztöne „abzieht“
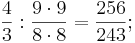
„In der folgenden Übersicht über die Intervalle der pythagoreischen Skala mit den entsprechenden mittelalterlichen Bezeichnungen sind die Zahlenverhältnisse vom Halbton bis zu Oktave zusammengestellt:
256 : 243 semitonium (Halbton)
9 : 8 tonus (Ganzton)
32 : 27 semiditonus (kleine Terz)
81 : 64 ditonus (große Terz)
4 : 3 diatessaron (Quarte)
729 : 512 tritonus (Tritonus)
3 : 2 diapente (Quinte)
128 : 81 semitonium et diapente (kleine Sexte)
27:16 tonus et diapente (große Sexte)
16:9 semiditonus et diapente (kleine Septime)
243:128 ditonus et diapente (große Septime)
2:1 diapason (Oktave)“[2]
Hier befinden sich einige Hörbeispiele zu den Intervallen bzw. Dreiklängen der pythagoreischen Stimmung:
| Halbton | Ganzton (Sekunde) | große Terz | Quarte | Quinte | große Sexte | große Septime | Oktave |
|---|---|---|---|---|---|---|---|
| 256 : 243 | 9 : 8 | 81 : 64 | 4 : 3 | 3 : 2 | 27:16 | 243:128 | 2 : 1 |
| media:256-243_Schritt.mp3 | media:pyth_Ganzton.mp3 | media:pyth_grT.mp3 | media:pythreinQuarte.mp3 | media:pythreinQuinte.mp3 | media:pythSexte.mp3 | media:pythSeptime.mp3 | media:Oktave.mp3 |
| Dur-Dreiklang | Moll-Dreiklang | pythagoreisches Komma | Dur-Tonleiter |
|---|---|---|---|
| 1 : 1; 81: 64; 3 : 2; | 1 : 1; 32: 27; 3 : 2; | ||
| media:Dur-Dreiklang.mp3 | media:Moll-Dreiklang.mp3 | media:pyth.komma.mp3 | media:Dur-Tonleiter.mp3 |
Das pythagoreische Komma
Nach der 12. Quinte sollte man eigentlich wieder beim Anfangston angelangt sein. 12 Quinten sollten 7 Oktaven entsprechen.
Jedoch gilt für 12 Quinten:
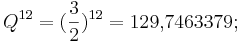
für 7 Oktaven gilt:
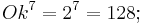
Man sieht, dass die 12 Quinten die 7 Oktaven übertreffen.
Das pythagoreische Komma entspricht dem Verhältnis der 12 Quinten zu den 7 Oktaven
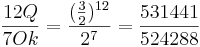
Für Interessierte: Der pythagoreische Quintenzirkel und Probleme des Systems
weiter zur reinen Stimmung
zur Übersicht



