Grundwissenübersicht: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 12: | Zeile 12: | ||
| − | == | + | ==Das Parallelogramm== |
Version vom 26. September 2010, 23:15 Uhr
Inhaltsverzeichnis |
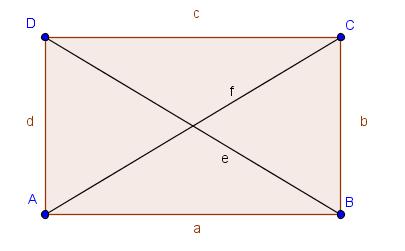
Das Rechteck
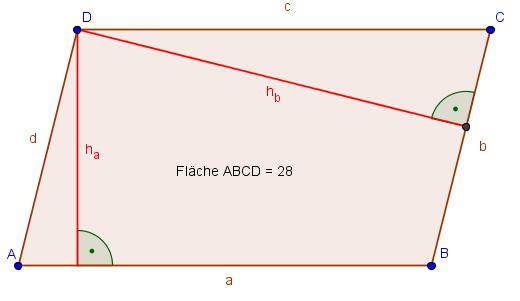
Das Parallelogramm
Das Dreieck
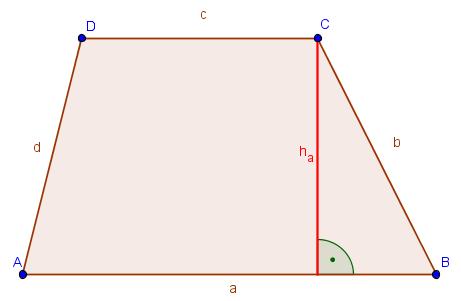
Das Trapez
|
Eigenschaften des Trapezes:
|
 a
a b
b
 .
.
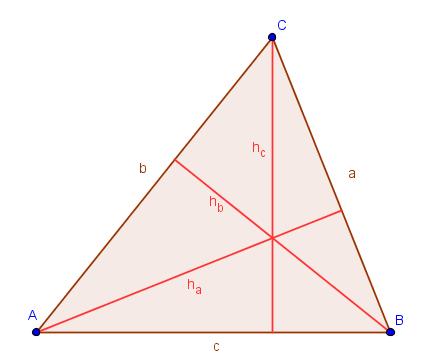
 ,
, 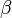 und
und 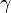 genannt.
genannt. 
