Flächenberechnung: Unterschied zwischen den Versionen
| Zeile 89: | Zeile 89: | ||
<br><br> | <br><br> | ||
<div align="center"><big><u style="color:green;background:green">Fläche=a<math>\cdot</math>h<sub>a</sub>=6<math>\cdot</math>4=24</u></big></div> | <div align="center"><big><u style="color:green;background:green">Fläche=a<math>\cdot</math>h<sub>a</sub>=6<math>\cdot</math>4=24</u></big></div> | ||
| + | |||
| + | <br> | ||
| + | <big>[[Lernpfad Flächenberechnung/Inhaltsverzeichnis/Parallelogramm/Flächenberechnung/Hefteintrag zum Parallelogramm|Hier]]</big> kommst du zum Hefteintrag. | ||
Version vom 11. August 2010, 13:35 Uhr
Flächenberechnung des Parallelogramms
Bevor wir uns Gedanken über die Fläche eines Parallelogramms machen, wollen wir uns erst einmal anschauen was ein Parallelogramm überhaupt ist und was es für Eigenarten hat. Dazu hab ich Behauptungen aufgestellt, die aber nicht alle auf das Parallelogramm zutreffen. Falls du dir nicht mehr ganz sicher bist wie das Parallelogramm aussieht kannst du unten nachkucken.
Behauptung 1:
Gegenüberliegende Winkel sind gleich groß.
(ja) (!nein)
Behauptung 2 :
Gegenüberliegende Winkel ergänzen sich zu 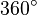 .
.
(!ja) (nein)
Behauptung 3:
Die Diagonalen im Parallelogramm halbieren sich gegenseitig.
(ja) (!nein)
Behauptung 4:
Gegenüberliegende Seiten sind parallel.
(ja) (!nein)
Behauptung 5:
Die Seiten eines Parallelogramms sind alle unterschiedlich lang.
(!ja) (nein)
Behauptung 6:
Rechteck und Quadrat sind besondere Parallelogramme.
(ja) (!nein)
Behauptung 7:
Gegenüberliegende Seiten sind gleich lang.
(ja) (!nein)
Behauptung 8:
Die Winkel im Paralleogramm betragen jeweils immer 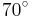
(!ja) (nein)
Behauptung 9:
Eine Diagonale teilt das Parallelogramm in zwei gleich große Dreiecke.
(ja) (!nein)
Eigenschaften des Parallelogramms:
- Gegenüberliegende Seiten sind parallel und gleich lang.
- Gegenüberliegende Winkel sind gleich groß.
- Je zwei benachbarte Winkel ergänzen sich zu
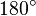 .
.
- Die Diagonalen halbieren sich gegenseitig.
- Jede Diagonale teilt das Parallelogramm in zwei gleich große Dreiecke.
- Rechteck und Quadrat sind spezielle Parallelogramme.
Die Fläche des Parallelogramms
Arbeitsaufträge:
- Ziehe den Punkt D so, dass du eine rechteckige Fläche bekommst, die du berechnen kannst. (Was fällt dir beim Flächeninhalt auf?)
- Drücke die Fläche des entstandenen Rechteckes mit Hilfe von a und ha aus.
- Versuche mit diesem Wissen die Flächenformel vom Parallelogramm zu erschließen.
Flächenformel durch makieren des grünen Feldes sichtbar machen!
 ha=6
ha=6 4=24
4=24
Hier kommst du zum Hefteintrag.

