2003 V: Unterschied zwischen den Versionen
| Zeile 71: | Zeile 71: | ||
<div align="right"><i>'''9 BE'''</i></div> | <div align="right"><i>'''9 BE'''</i></div> | ||
<br> | <br> | ||
| − | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
}} | }} | ||
| + | |||
e) Die Punkte S<sub>a</sub> bilden in H eine Kurve. Diese wird parallel zur | e) Die Punkte S<sub>a</sub> bilden in H eine Kurve. Diese wird parallel zur | ||
| Zeile 81: | Zeile 81: | ||
<div align="right"><i>'''8 BE'''</i></div> | <div align="right"><i>'''8 BE'''</i></div> | ||
<br> | <br> | ||
| − | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
}} | }} | ||
| Zeile 104: | Zeile 103: | ||
<div align="right"><i>'''5 BE'''</i></div> | <div align="right"><i>'''5 BE'''</i></div> | ||
<br> | <br> | ||
| − | |||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
}} | }} | ||
| + | |||
b) Das Sechseck ABCDEF rotiert nun um die Achse AD.Beschreiben Sie das Aussehen des dabei entstehenden Rotationskörpers. Ermitteln Sie eine Gleichung der kleinsten Kugel, die den Rotationskörper enthält. | b) Das Sechseck ABCDEF rotiert nun um die Achse AD.Beschreiben Sie das Aussehen des dabei entstehenden Rotationskörpers. Ermitteln Sie eine Gleichung der kleinsten Kugel, die den Rotationskörper enthält. | ||
Liegt der Ursprung des Koordinatensystems innerhalb oder außerhalb dieses Rotationskörpers? Begründen Sie Ihre Antwort. | Liegt der Ursprung des Koordinatensystems innerhalb oder außerhalb dieses Rotationskörpers? Begründen Sie Ihre Antwort. | ||
Version vom 13. April 2010, 13:22 Uhr
Bitte Link zu den Originalaufgaben ausbessern und Gesamtlösung hochladen
|
|
|
In einem kartesischen Koordinatensystem des
|
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft. 3 BE
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau. 6 BE
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ] 3 BE
9 BE
8 BE
|
Ferner sind die Punkte A ( 1 / 6 / 1) und B (-2 / 9 / 1) gegeben.
5 BE
6 BE
|
 3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 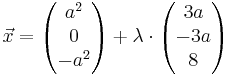 ,
, 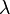 ∈
∈ 
