2003 V: Unterschied zwischen den Versionen
| Zeile 14: | Zeile 14: | ||
<center>Erarbeitet von Nellie Kirchner, Lea Mainberger, Maximilian Benkert</center> | <center>Erarbeitet von Nellie Kirchner, Lea Mainberger, Maximilian Benkert</center> | ||
| − | + | ||
| Zeile 26: | Zeile 26: | ||
In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die | In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die | ||
| − | Ebene H: x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> - 8 = 0 , sowie die Schar von Geraden g<sub>a</sub> : <math>\vec x = \begin{pmatrix} a^2 \\ 0 \\ -a^2 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3a \\ -3a \\ 8 \end{pmatrix}</math>, <math>\lambda</math> ∈ <math>\mathbb{R </math>, a ∈ <math>\mathbb{R </math> gegeben. | + | Ebene H: x<sub>1</sub> + x<sub>2</sub> + x<sub>3</sub> - 8 = 0 , sowie die Schar von Geraden g<sub>a</sub> : <math>\vec x = \begin{pmatrix} a^2 \\ 0 \\ -a^2 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3a \\ -3a \\ 8 \end{pmatrix}</math>, <math>\lambda</math> ∈ <math>\mathbb{R} </math> , a ∈ <math>\mathbb{R} </math> gegeben. |
| Zeile 45: | Zeile 45: | ||
<br> | <br> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| + | }} | ||
| Zeile 53: | Zeile 54: | ||
<div align="right"><i>'''6 BE'''</i></div> | <div align="right"><i>'''6 BE'''</i></div> | ||
<br> | <br> | ||
| − | :{{Lösung versteckt| | + | :{{Lösung versteckt| |
| − | + | ||
}} | }} | ||
| Zeile 65: | Zeile 65: | ||
<br> | <br> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | }} | |
| Zeile 74: | Zeile 74: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | }} | |
e) Die Punkte S<sub>a</sub> bilden in H eine Kurve. Diese wird parallel zur | e) Die Punkte S<sub>a</sub> bilden in H eine Kurve. Diese wird parallel zur | ||
| Zeile 84: | Zeile 84: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | }} | |
Version vom 13. April 2010, 13:15 Uhr
Bitte Link zu den Originalaufgaben ausbessern und Gesamtlösung hochladen
|
|
|
In einem kartesischen Koordinatensystem des
|
a) Zeigen Sie, dass keine der Geraden ga parallel und keine senkrecht zur Ebene H verläuft. 3 BE
b) Welche dieser Geraden schneidet H unter dem größten Winkel? Berechnen Sie diesen maximalen Winkel auf eine Dezimale genau. 6 BE
[ Zur Kontrolle: Sa = (a2 + 3a / -3a / 8 - a2) ] 3 BE
9 BE
e) Die Punkte Sa bilden in H eine Kurve. Diese wird parallel zur x3-Achse in die x1x2-Ebene projiziert; die Projektion heißt P. Fertigen Sie eine Zeichnung von P in der x1x3-Ebene an. Um welchen Kurventyp handelt es sich bei P vermutlich? Überprüfen Sie Ihre Vermutung, indem Sie eine Koordinatengleichung von P aufstellen. 8 BE
|
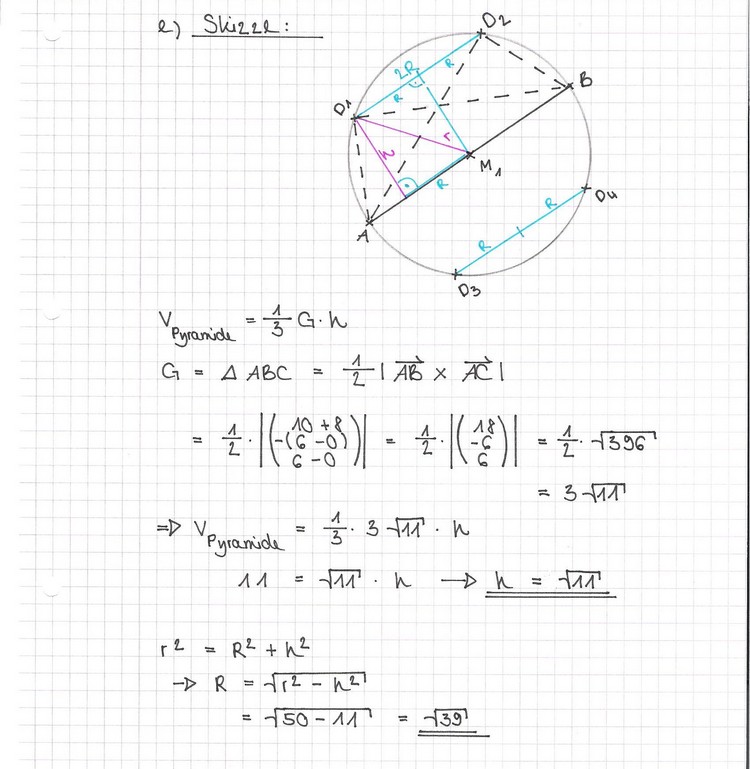
Die Ebene E ist Tangentialebene an zwei Kugeln K1 und K2 mit dem Radius
[Teilergebnis: M1 = (2/5/-6)] 6 BE
b) Die Kugelpunkte P 3 BE
der x2 -Wert von M2 ist falsch (-5/3) Der Vektor M1M2 wurde in der anderen aufgestellt in der er berechnet wurde.
4 BE
[Teilergebnis: B (5/10/-10)] 4 BE
[Zur Kontrolle: h = 6 BE
|
 3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga :
3 ist die
Ebene H: x1 + x2 + x3 - 8 = 0 , sowie die Schar von Geraden ga : 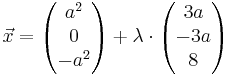 ,
,  ∈
∈  , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
 K1 und Q
K1 und Q 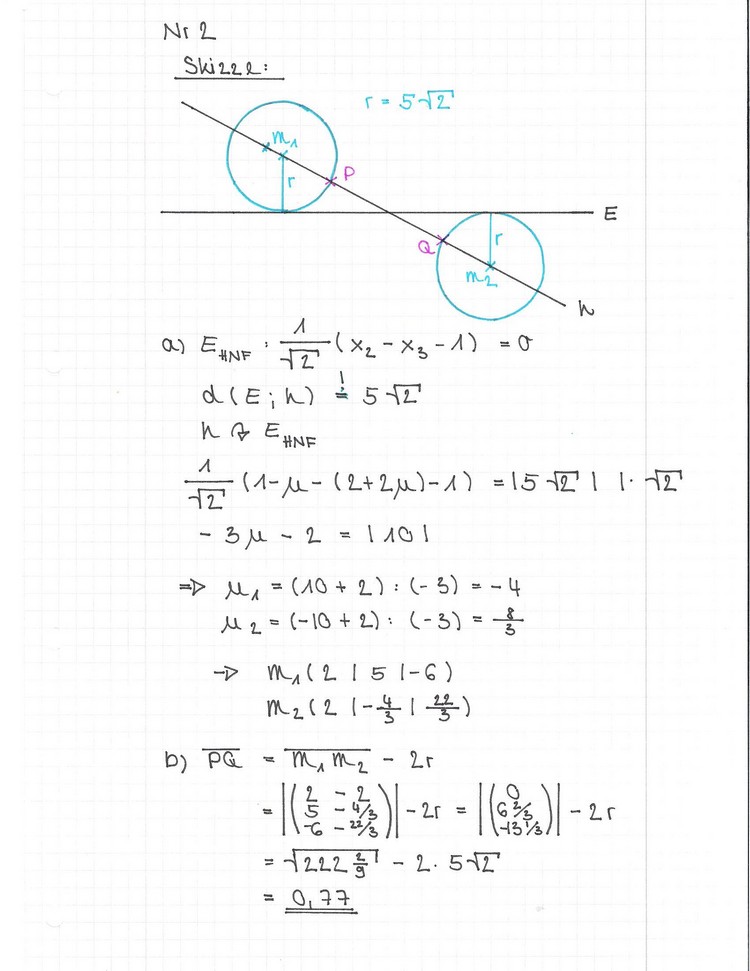
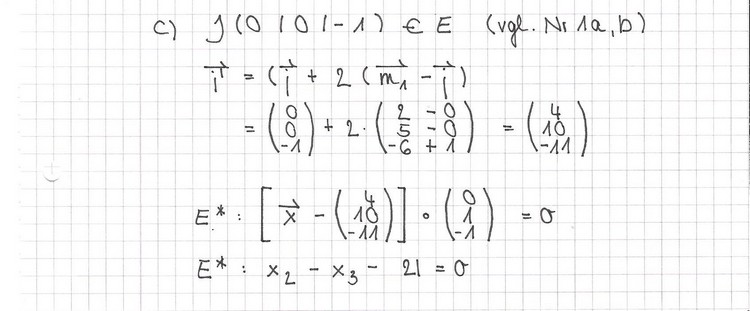

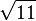 ]
]