2003 I: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 92: | Zeile 92: | ||
[Ergebnis: <math>x_{1/2}=ln(m\pm\sqrt{m^2-1}</math>] | [Ergebnis: <math>x_{1/2}=ln(m\pm\sqrt{m^2-1}</math>] | ||
| − | + | ||
| + | |||
| + | <popup name="Tipp"> | ||
[[Bild:Abi_2003_I_2a_Tipp.png|700px]] | [[Bild:Abi_2003_I_2a_Tipp.png|700px]] | ||
| − | + | </popup> | |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
[[Bild:Abi_2003_I_Lösung_2a.png|700px]] | [[Bild:Abi_2003_I_Lösung_2a.png|700px]] | ||
| + | [[Bild:Abi_2003_I_2a_Zusatz.png|700px]] | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
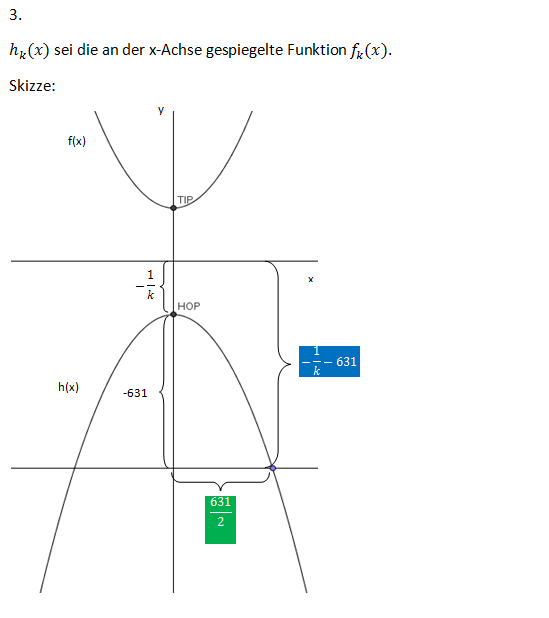
;b) Lässt man das im 1. Quadranten liegende, von G<sub>1</sub>, der positiven y-Achse und der Geraden mit der Gleichung y = 10 begrenzte Flächenstück um die y-Achse rotieren, entsteht ein kelchförmiger Körper. Berechnen Sie dessen Durchmesser d am oberen Rand. | ;b) Lässt man das im 1. Quadranten liegende, von G<sub>1</sub>, der positiven y-Achse und der Geraden mit der Gleichung y = 10 begrenzte Flächenstück um die y-Achse rotieren, entsteht ein kelchförmiger Körper. Berechnen Sie dessen Durchmesser d am oberen Rand. | ||
; Geben Sie einen Ansatz für das Volumen V des Kelches an (Berechnung ist nicht verlangt). <div align="right">''5 BE''</div> | ; Geben Sie einen Ansatz für das Volumen V des Kelches an (Berechnung ist nicht verlangt). <div align="right">''5 BE''</div> | ||
| − | + | <popup name="Tipp"> | |
[[Bild:Abi_2003_I_2b_Tipp.png|700px]] | [[Bild:Abi_2003_I_2b_Tipp.png|700px]] | ||
| − | + | </popup> | |
| Zeile 135: | Zeile 134: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
[[Bild:Abi_2003_I_3_Skizze.png|700px]] | [[Bild:Abi_2003_I_3_Skizze.png|700px]] | ||
| + | [[Bild:Abi_2003_I_Lösung_3.png|700px]] | ||
}} | }} | ||
| − | |||
| − | |||
| − | |||
| − | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Aktuelle Version vom 11. April 2010, 16:57 Uhr
|
|
g: x →
Hinweis: Die Entstehung von Graphen aus anderen Graphen kann in diesem Lernpfad wiederholt werden.
|
[Ergebnis:
|
|
 definierten Funktionen
definierten Funktionen 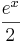 , g*:x →
, g*:x → 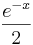 und f1: x →
und f1: x → 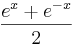 .
.
 x
x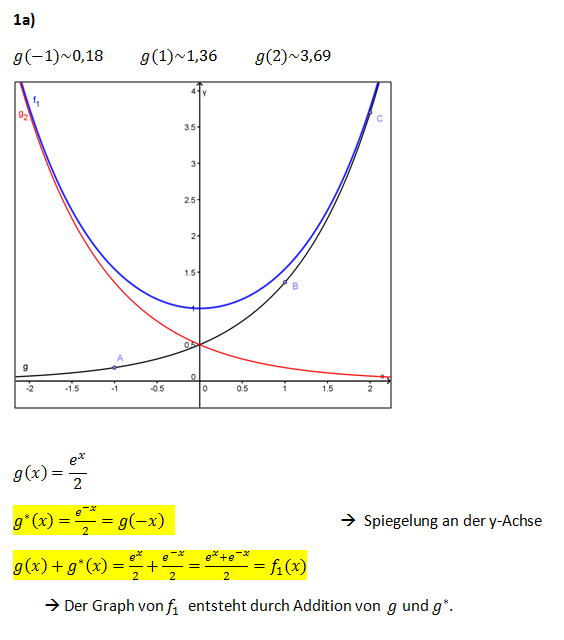
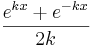 mit D =
mit D = 

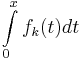 mit dem Definitionsbereich
mit dem Definitionsbereich 
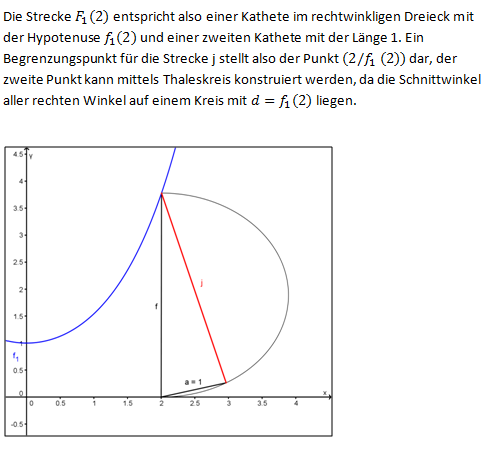
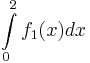 als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig.
als Streckenlänge in Ihrer Zeichnung und markieren Sie die zugehörige Strecke farbig. 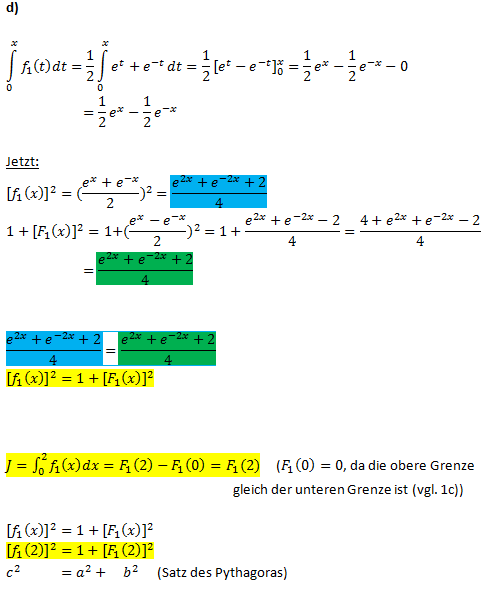
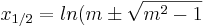 ]
]