2003 II: Unterschied zwischen den Versionen
| Zeile 30: | Zeile 30: | ||
<math>G_k\,</math> bezeichnet.<br /> | <math>G_k\,</math> bezeichnet.<br /> | ||
| − | a) Geben Sie <math>f_k (0)\,</math> sowie die Nullstelle von <math>f_k\,</math> an. | + | a) Geben Sie <math>f_k(0)\,</math> sowie die Nullstelle von <math>f_k\,</math> an. |
Untersuchen Sie das Verhalten von <math> f_k\,</math> für <math>x\rightarrow -\infty</math> und für <math>x\rightarrow +\infty</math> br /> | Untersuchen Sie das Verhalten von <math> f_k\,</math> für <math>x\rightarrow -\infty</math> und für <math>x\rightarrow +\infty</math> br /> | ||
Version vom 9. April 2010, 12:40 Uhr
|
|
|
Aufgabe 1 Gegeben ist die Schar der in IR definierten Funktionen
a) Geben Sie
b) Zeigen Sie, dass f (x) 2 fk 2(x) 1 k′ =k′ = − gilt, und ermitteln Sie hiermit Funktionsterme der Ableitungen fk′′ und fk′′′ sowie einer Stammfunktion von fk .
c) Zeigen Sie, dass Gk genau einen Hochpunkt und genau einen Wendepunkt besitzt, und bestimmen Sie die Koordinaten dieser Punkte.
|
|
Aufgabe 2 Das abgebildete Zelt - geometrisch betrachtet ein gerades Prisma - hat einen rechteckigen Grundriss mit den Seitenlängen a 2 3 und b. Die Front besteht aus einem Rechteck mit den Seitenlängen a 2 3 und a sowie einem aufgesetzten gleichschenkligen Dreieck der Höhe a. a) Zeigen Sie, dass für den Rauminhalt V des Zelts und für den Flächeninhalt S der benötigten Zeltplane (ohne Boden und Laschen, das Zelt ist vollständig geschlossen) gilt: V a b , S a ab 2 2 9 2 2 9 4 = 9 = + .
b) Bestimmen Sie a und b so, dass V = 121,5 m3 ist und dass der Materialverbrauch an Zeltplane möglichst gering ist. Wie viele m2 Zeltplane werden in diesem Fall benötigt?
|
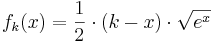 mit
mit 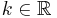 . Der jeweilige Graph von Fehler beim Parsen(Lexikalischer Fehler): f_k\
, wird mit
. Der jeweilige Graph von Fehler beim Parsen(Lexikalischer Fehler): f_k\
, wird mit
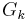 bezeichnet.
bezeichnet.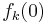 sowie die Nullstelle von
sowie die Nullstelle von 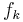 an.
Untersuchen Sie das Verhalten von
an.
Untersuchen Sie das Verhalten von 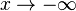 und für
und für 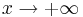 br />
br />

