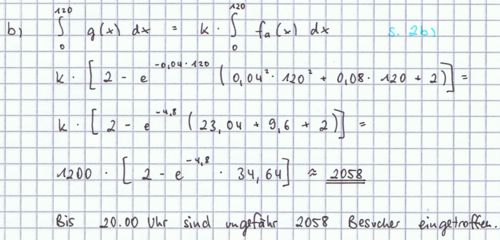2009 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(BE eingefügt) |
(Bilder eingefügt) |
||
| Zeile 33: | Zeile 33: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_1a_Lös.jpg|500px]] |
}} | }} | ||
| Zeile 42: | Zeile 42: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_1b_Lös.jpg|500px]] |
}} | }} | ||
| Zeile 63: | Zeile 63: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_2a_Lös.jpg|500px]] |
}} | }} | ||
| Zeile 72: | Zeile 72: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_2b_Lös.jpg|500px]] |
}} | }} | ||
| Zeile 81: | Zeile 81: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_2c_Lös.jpg|500px]] |
}} | }} | ||
| Zeile 102: | Zeile 102: | ||
a) Bestimmen Sie die Parameter a und k, wenn das Maximum der Funktion g um 18.50 Uhr auftritt und 26 Besucher pro Minute beträgt.<div align="right">''5 BE''</div> | a) Bestimmen Sie die Parameter a und k, wenn das Maximum der Funktion g um 18.50 Uhr auftritt und 26 Besucher pro Minute beträgt.<div align="right">''5 BE''</div> | ||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI_2009_II_3a_Lös.jpg|500px]] | ||
| + | |||
| + | }} | ||
| Zeile 108: | Zeile 113: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild: | + | [[Bild:ABI_2009_II_3b_Lös.jpg|500px]] |
}} | }} | ||
Version vom 1. April 2010, 10:41 Uhr
|
|
Gegeben ist die Schar der Funktionen
3 BE
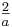 ] ]7 BE
|
Nun werden die in IR definierten Integralfunktionen 4 BE
10 BE
6 BE
|
Die Gruppe „Die toten Rosen“ gibt ein Konzert. Es beginnt um 20 Uhr, der Einlass wird ab 18 Uhr gewährt. Der Besucherzustrom soll durch eine Funktion g der Form g(x) = k ⋅ fa (x) mit geeignetem a und geeignetem k > 0 modelliert werden. Dabei bedeutet x die seit 18 Uhr vergangene Zeit in Minuten. g(x) gibt die momentane Zunahme der Besucherzahl in Besucher pro Minute an.
5 BE
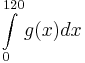 und interpretieren Sie das Ergebnis im Anwendungszusammenhang. und interpretieren Sie das Ergebnis im Anwendungszusammenhang.5 BE
|
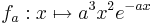 mit a ∈ IR+ und der Definitionsmenge IR . Der Graph von fa wird mit Ga bezeichnet. Die Abbildung zeigt Ga für a = 0,04.
mit a ∈ IR+ und der Definitionsmenge IR . Der Graph von fa wird mit Ga bezeichnet. Die Abbildung zeigt Ga für a = 0,04.
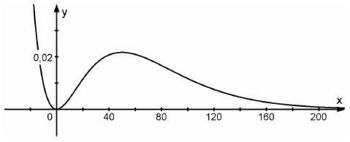


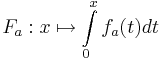 betrachtet.
betrachtet.