2007 VI: Unterschied zwischen den Versionen
(Dateilinks eingefügt//) |
|||
| Zeile 38: | Zeile 38: | ||
[mögliches Teilergebnis: E<sub>t</sub> : 2x<sub>1</sub> + x<sub>2</sub> - 2x<sub>3</sub> - t = 0] | [mögliches Teilergebnis: E<sub>t</sub> : 2x<sub>1</sub> + x<sub>2</sub> - 2x<sub>3</sub> - t = 0] | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:1 a1 -.jpg|800px]] | ||
| + | }} | ||
b) Berechnen Sie den Winkel φ, unter dem jede Ebene der Schar E<sub>t</sub> die x<sub>1</sub>x<sub>2</sub>-Ebene schneidet, auf eine Dezimale gerundet. | b) Berechnen Sie den Winkel φ, unter dem jede Ebene der Schar E<sub>t</sub> die x<sub>1</sub>x<sub>2</sub>-Ebene schneidet, auf eine Dezimale gerundet. | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:1 b --.jpg|800px]] | ||
| + | }} | ||
| Zeile 50: | Zeile 54: | ||
[mögliches Teilergebnis: L: x<sub>1</sub> + x<sub>3</sub> = 0] | [mögliches Teilergebnis: L: x<sub>1</sub> + x<sub>3</sub> = 0] | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:1 c.jpg|800px]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 70: | Zeile 76: | ||
[Teilergebnis: A<sub>t</sub> (0,5t|0|0); B<sub>t</sub> (0|t|0); C<sub>t</sub> (0|0|-0,5t)] | [Teilergebnis: A<sub>t</sub> (0,5t|0|0); B<sub>t</sub> (0|t|0); C<sub>t</sub> (0|0|-0,5t)] | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:2 a1.jpg|800px]] | ||
| + | [[Bild:2 a2.jpg|800px]] | ||
| + | }} | ||
b) Zeigen Sie, dass die Pyramide II<sub>t</sub> den Oberflächeninhalt t<sup>2</sup> besitzt, und ermitteln Sie das Volumen V<sub>t</sub> von II<sub>t</sub> in Abhängigkeit von t. | b) Zeigen Sie, dass die Pyramide II<sub>t</sub> den Oberflächeninhalt t<sup>2</sup> besitzt, und ermitteln Sie das Volumen V<sub>t</sub> von II<sub>t</sub> in Abhängigkeit von t. | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:2 b1.jpg|800px]] | ||
| + | [[Bild:2 b2.jpg|800px]] | ||
| + | [[Bild:2 b3.jpg|800px]] | ||
| + | }} | ||
c) Die Ebene F : 2x<sub>2</sub> = t liegt parallel zu einer Seitenfläche und zerlegt II<sub>t</sub> in zwei Teilkörper. Berechnen Sie das Verhältnis der Volumina. | c) Die Ebene F : 2x<sub>2</sub> = t liegt parallel zu einer Seitenfläche und zerlegt II<sub>t</sub> in zwei Teilkörper. Berechnen Sie das Verhältnis der Volumina. | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:2 c1.jpg|800px]] | ||
| + | [[Bild:2 c2.jpg|800px]] | ||
| + | }} | ||
d) Zeigen Sie, dass die Kugel K mit dem Mittelpunkt N<sub>t</sub> (<math>\frac{t}{8}</math> |<math>\frac{t}{8}</math> |<math>\frac{-t}{8}</math> ) und dem Radius ρ<sub>t</sub> = <math>\frac{|t|}{8}</math> die Inkugel der Pyramide II<sub>t</sub> ist, also alle Begrenzungsflächen von II<sub>t</sub> von innen berührt. | d) Zeigen Sie, dass die Kugel K mit dem Mittelpunkt N<sub>t</sub> (<math>\frac{t}{8}</math> |<math>\frac{t}{8}</math> |<math>\frac{-t}{8}</math> ) und dem Radius ρ<sub>t</sub> = <math>\frac{|t|}{8}</math> die Inkugel der Pyramide II<sub>t</sub> ist, also alle Begrenzungsflächen von II<sub>t</sub> von innen berührt. | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:2 d1.jpg|800px]] | ||
| + | [[Bild:2 d2.jpg|800px]] | ||
| + | [[Bild:2 d3.jpg|800px]] | ||
| + | [[Bild:2 d4.jpg|800px]] | ||
| + | }} | ||
| Zeile 94: | Zeile 115: | ||
Geben Sie m<sub>1</sub> sowie m<sub>3</sub> an und berechnen Sie r. | Geben Sie m<sub>1</sub> sowie m<sub>3</sub> an und berechnen Sie r. | ||
| − | :{{Lösung versteckt|}} | + | :{{Lösung versteckt| |
| + | [[Bild:2 e.jpg|800px]] | ||
| + | }} | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 24. Februar 2010, 17:47 Uhr
|
|
In einem kartesischen Koordinatensystem des IR3 ist die Ebenenschar Et : 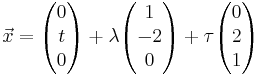 mit λ, τ є IR und t є IR gegeben. mit λ, τ є IR und t є IR gegeben. |
a) Bestimmen Sie eine Gleichung von Et in Normalenform. Begründen Sie, dass alle Ebenen der Schar zueinander parallel sind. [mögliches Teilergebnis: Et : 2x1 + x2 - 2x3 - t = 0]
[mögliches Teilergebnis: L: x1 + x3 = 0] |
Die Ebene Et schneidet die x1-Achse im Punkt At, die x2-Achse im Punkt Bt und die x3-Achse im Punkt Ct. Diese Punkte und der Ursprung O sind für t ≠ 0 die Ecken einer Pyramide IIt.
[Teilergebnis: At (0,5t|0|0); Bt (0|t|0); Ct (0|0|-0,5t)]
Begründen Sie ohne weitere Rechnung, dass gilt: m2 = Geben Sie m1 sowie m3 an und berechnen Sie r. |









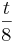 |
|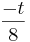 ) und dem Radius ρt =
) und dem Radius ρt = 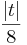 die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt.
die Inkugel der Pyramide IIt ist, also alle Begrenzungsflächen von IIt von innen berührt.




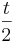 .
.


