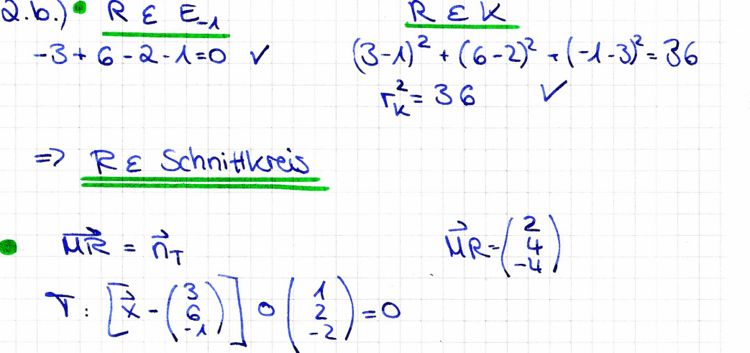2007 V: Unterschied zwischen den Versionen
K |
K (gesamte Loesung) |
||
| Zeile 14: | Zeile 14: | ||
<center>'''Lösung von Ruth Burkard, Julian Weinbeer und Veronika Weinbeer'''</center> | <center>'''Lösung von Ruth Burkard, Julian Weinbeer und Veronika Weinbeer'''</center> | ||
<br> | <br> | ||
| + | |||
| + | [[Media:Abi_2007_V_gesamte_Loesung.doc|gesamte Lösung]] | ||
| + | |||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 22. Februar 2010, 18:36 Uhr
|
|
Gegeben ist in einem kartesischen Koordinatensystem des IR3 die Ebenenschar Ek : kx1 + k 2x2 + 2x3- k2 = 0 , mit k ∈ IR als Scharparameter.
a) Ermitteln Sie, für welche Werte von k die Ebene Ek den Punkt P(1|2|-3)und zugleich den Punkt Q(0|1|0) enthält. 4 BE
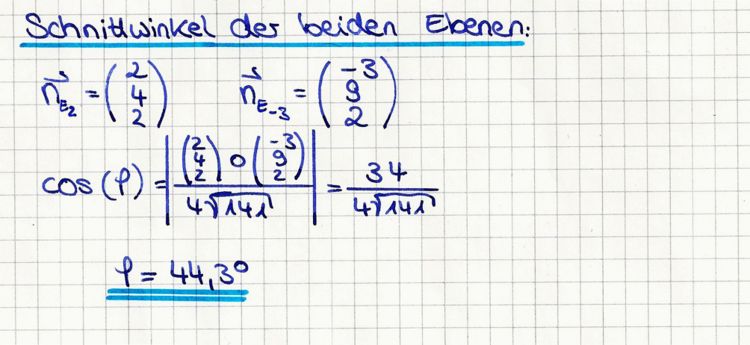
b) Die beiden Ebenen E2 und E-3 schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und
[mögliches Teilergebnis: g:
5 BE
4 BE
5 BE
e) Untersuchen Sie, ob die Gerade g aus Teilaufgabe 1b senkrecht auf einer Ebene der Schar Ek steht. 3 BE
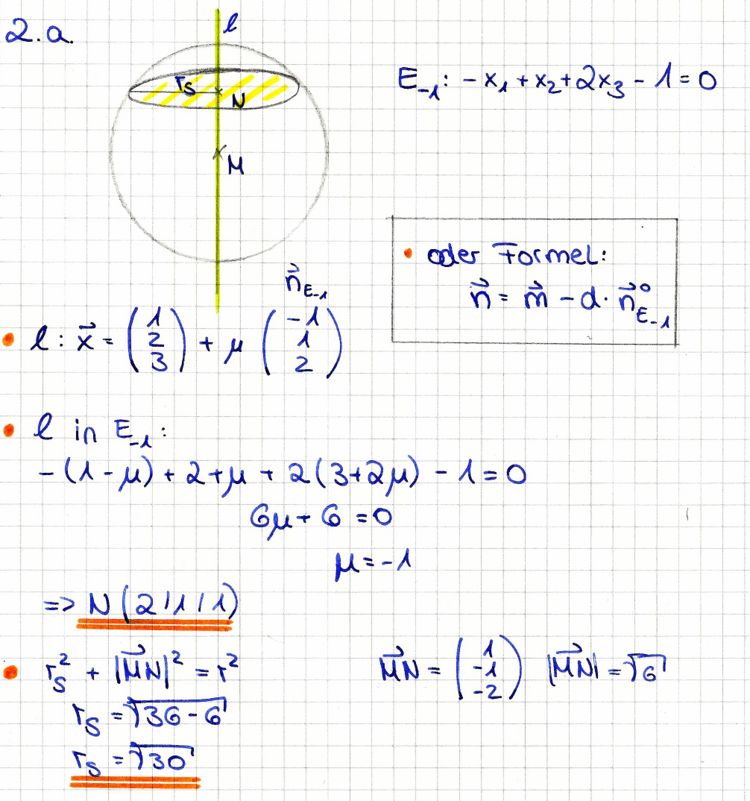
Nun ist weiter die Kugel K mit dem Mittelpunkt M(1|2|3) und dem Radius r= 6 gegeben. Die Scharebene E-1 schneidet die Kugel K in einem Kreis ks mit dem Mittelpunkt N und dem Radius rs. a) Berechnen Sie die Koordinaten N und den Radius rs
6 BE
b) Zeigen Sie, dass der Punkt R(3|6|-1) auf dem Schnittkreis ks liegt, und stellen Sie eine Gleichung der Tangentialebene T
4 BE
c) Die Ebene E-1 und die Tangentialebene an die Kugel K in allen Punkten des Schnittkreises ks begrenzen einen geraden
5 BE
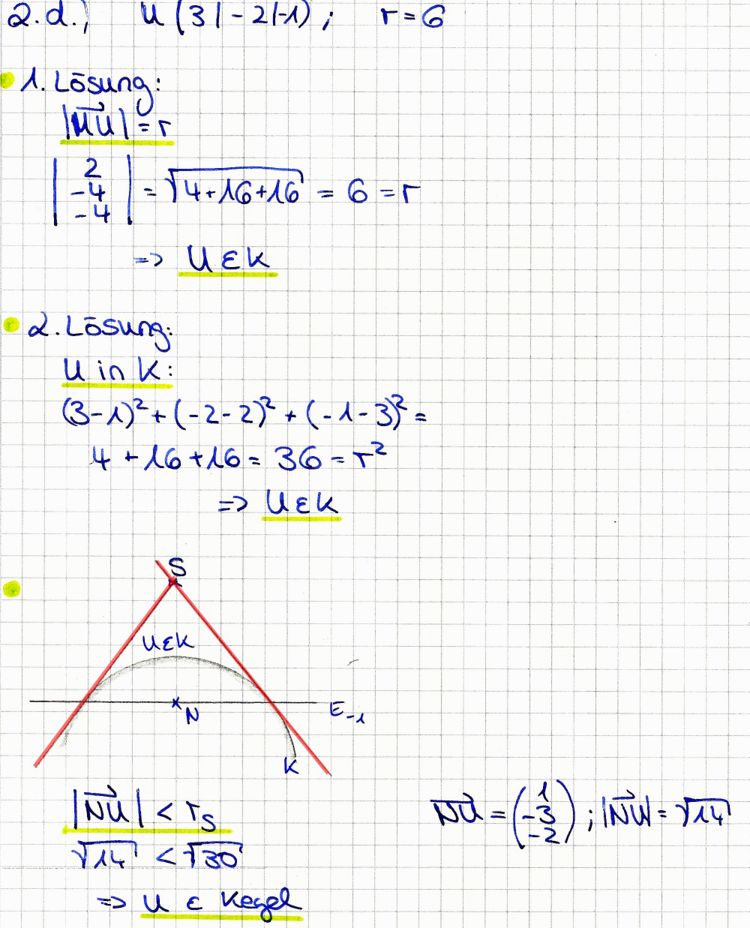
d) Zeigen Sie, dass der Punkt U(3|-2|-1) auf der Kugel K und innerhalb des Kreiskegels liegt. 4 BE
|

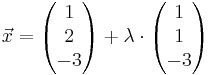 , λ ∈ IR ]
, λ ∈ IR ]


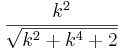 und dass e(k)<1 ist.
und dass e(k)<1 ist.


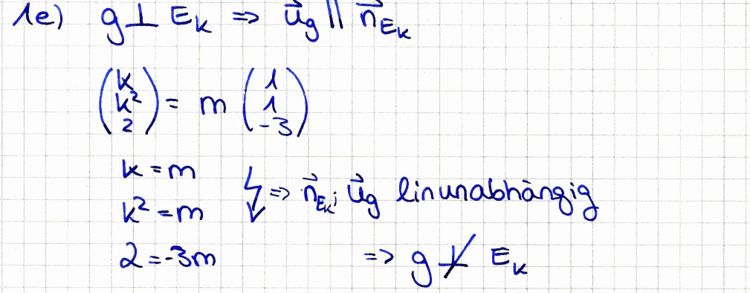
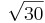 ]
]