2006 III: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 110: | Zeile 110: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:Abi2006StochIIIaufgabe3b2.jpeg| | + | [[Bild:Abi2006StochIIIaufgabe3b2.jpeg|5px]] |
}} | }} | ||
| Zeile 125: | Zeile 125: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| − | Sei H die relative Häufigkeit der Anzahl der Treffer einer nach B(n, p) verteilten Zufallsgröße. Geben Sie den Erwartungswert von H an und zeigen Sie, dass die Standardabweichung von H kleiner oder gleich | + | Sei H die relative Häufigkeit der Anzahl der Treffer einer nach B(n, p) verteilten Zufallsgröße. Geben Sie den Erwartungswert von H an und zeigen Sie, dass die Standardabweichung von H kleiner oder gleich ist. ''4 BE'' |
| − | ist. ''4 BE'' | + | |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
Version vom 20. Februar 2010, 17:58 Uhr
|
|
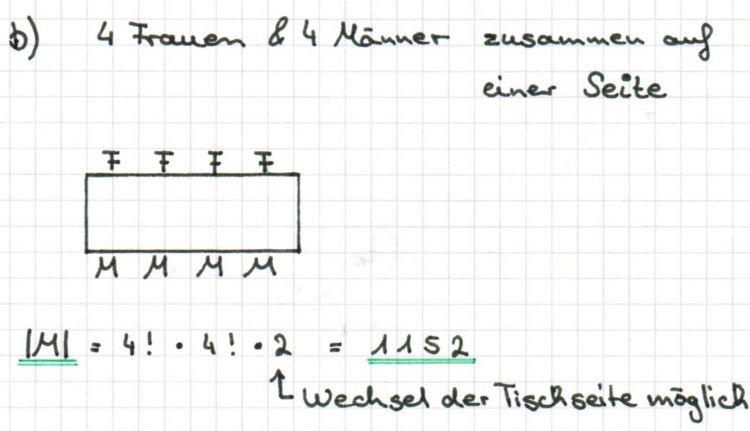
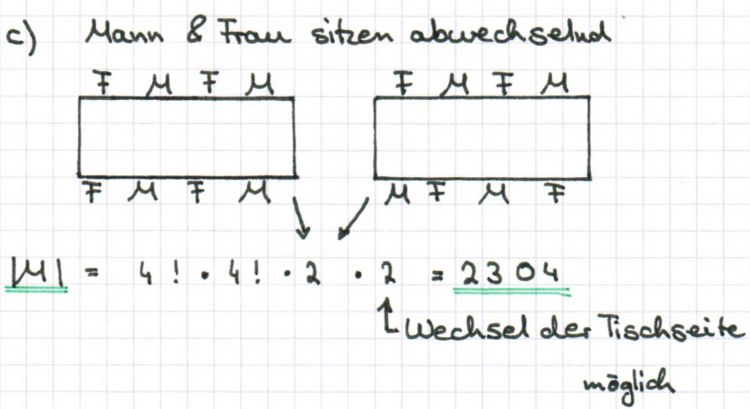
Für einen 8-köpfigen Ausschuss kandidieren 12 Frauen und 8 Männer. a) Wie viele Möglichkeiten gibt es, den Ausschuss zusammenzusetzen, wenn er mindestens 3 und höchstens 5 männliche Mitglieder haben soll? 4 BE b) Auf wie viele verschiedene Arten können die Ausschussmitglieder Platz nehmen, wenn die 4 Frauen auf einer Seite des Tisches sitzen sollen und die Personen unterschieden werden? 3 BE c) Auf wie viele verschiedene Arten können die Ausschussmitglieder Platz nehmen, wenn auf jeder Längsseite des Tisches Frauen und Männer abwechselnd sitzen sollen und die Personen unterschieden werden? 4 BE
|
Beim Abiturstreich an einem Gymnasium muss ein Sportlehrer seine Sicherheit bei Basketball-Freiwürfen gegen einen Vereinsspieler aus dem Kreis der Abiturienten unter Beweis stellen. Der Sportlehrer trifft bei jedem Versuch mit einer Wahrscheinlichkeit von 35 %, der Vereinsspieler mit einer Wahrscheinlichkeit von 60 %. a) Mit welcher Wahrscheinlichkeit trifft der Sportlehrer bei 12 Versuchen höchstens zweimal? 4 BE b) Der Sportlehrer hat bei seinen 12 Versuchen dreimal getroffen. Wie oft muss der Vereinsspieler mindestens werfen, damit er mit einer Wahrscheinlichkeit von mindestens 80 % mehr als 3 Treffer erzielt? Verwenden Sie zur Lösung die Tabellen zur Stochastik. 4 BE c) Wie oft muss die Schulleiterin, die im Mittel bei jedem 8. Wurf in den Korb trifft, mindestens werfen, um mit einer Wahrscheinlichkeit von mehr als 90 % wenigstens einmal zu treffen? 4 BE d) Ein Schüler führt 100 Freiwürfe aus, um seine Trefferwahrscheinlichkeit p zu bestimmen. Als Ergebnis möchte er ein Intervall angeben, in dem p mit einer Wahrscheinlichkeit von mindestens 75 % liegt. Zeigen Sie, dass die Länge dieses Intervalls nicht kleiner als gewählt werden kann, wenn diese mit der Ungleichung von Tschebyschow abgeschätzt wird. 4 BE
|
Ein Prüfer einer Universität entwickelt einen Multiple-Choice-Test, der aus 50 Fragen mit je 4 Antworten besteht, von denen jeweils genau eine richtig ist. Für das Bestehen des Tests legt er die Mindestzahl richtiger Antworten nach folgendem Kriterium fest: Wenn ein Student durch sein Wissen nur die Hälfte der Fragen sicher richtig beantworten kann und die übrigen Fragen ausschließlich aufgrund bloßen Ratens beantwortet, dann soll er den Test mit einer Wahrscheinlichkeit von mindestens 95 % nicht bestehen. a) Bestimmen Sie, wie viele Fragen mindestens richtig beantwortet werden müssen, damit der Test unter den genannten Bedingungen bestanden wird. 5 BE b) Ein Student kann 60 % der Fragen durch sein Wissen sicher beant-worten und muss sich beim Rest auf bloßes Raten verlassen. Mit welcher Wahrscheinlichkeit besteht er den Test nicht, wenn für das Bestehen mindestens 36 Fragen richtig beantwortet werden müssen? 4 BE |